JEE 2012 :: General Questions :: Mathematics

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics

Tangents are drawn to the hyperbola $\frac{x^{2}}{9}-\frac{y^{2}}{4}=1$ parallel to the straight line 2x-y=1.The points of contacts of the tangents on the hyperbola are

Answer:

Explanation:

Concept lnvolved

Equation of tangent   to $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ is

  $y= mx \pm \sqrt{a^{2}m^{2}-b^{2}}$

Description of Situation If two straight
lines

  $a_{1}x+b_{1}y+c_{1}=0$

 and $ax_{2}+b_{2}y+c_{2}=0$ are identical

 $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

 sol., Equation of tangent   , parallel to 

 y=2x-1

 $\Rightarrow$   $y=2x\pm\sqrt{9(4)-4}$

 $\therefore$   $y =2x \pm \sqrt{32}$....(i)

 The equation of tangent at $(x_{1},y_{1})$ is 

 $\frac{xx_{1}}{9}-\frac{yy_{1}}{4}=1$ ...(ii)

from Eqs(i) and (ii) , we get 

 $\frac{2}{\frac{x_{1}}{9}}=\frac{-1}{\frac{-y_{1}}{4}}=\frac{\pm\sqrt{32}}{1}$

$\Rightarrow$     $x_{1}=-\frac{9}{2\sqrt{2}} and y_{1}=-\frac{1}{\sqrt{2}}$

 or   $x_{1}=\frac{9}{2\sqrt{2}}$ and  $y_{1}=\frac{1}{\sqrt{2}}$

If S be the area of the region enclosed   by $y^{e^{-x^{2}}}$, y=0,x=0 and x=1 , then

Answer:

Explanation:

Concept  involved
(i) Area of region f(x) bounded between x=a to x=b is

 $\int_{a}^{b} f(x) dx=$ sum of areas of rectangle  shown in shaded part

 (ii) if $f(x)  \geq g(x)$ when defined in [a, b]

$\Rightarrow$   $\int_{a}^{b} f(x) dx \geq\int_{a}^{b} g(x) dx$

Description of Situation As the given curve y =$e^{-x^{2}}$  cannot be integrated thus we
have to bound this function by using above  mentioned concept 

 sol. Graph for , $y=e^{-x^{2}}$

 since , $x^{2} \leq x$ when $x \epsilon [0,1]$

 $\Rightarrow$  $-x^{2} \geq  -x$ or $e^{-x^{2}} \geq e^{-x}$

$\therefore$     $\int_{0}^{1} e^{-x^{2}} dx \geq \int_{0}^{1} e^{-x} dx$

 $\Rightarrow$  $S\geq -(e^{-x})_{0}^{1} =1-\frac{1}{e}$........(i)

 Also, $\int_{0}^{1} e^{-x^{2}} dx \leq$ area of two rectangle 

 $\leq \left(1\times \frac{1}{\sqrt{2}}\right)+\left(1-\frac{1}{\sqrt{2}}\right)\times\frac{1}{\sqrt{e}}$

$\leq \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{e}}\left(1-\frac{1}{\sqrt{2}}\right)$..........(ii)

$\therefore$  $\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{e}}\left(1-\frac{1}{\sqrt{2}}\right)\geq S \geq1-\frac{1}{e}$

 [from Eqs.(i) and (ii) ]

Let $\theta$ , $\phi \epsilon [0,2\pi]$ be such that $2 \cos \theta(1-\sin \phi)=\sin^{2} \theta$

$\left( \tan \frac{\theta}{2}+\cot \frac{\theta}{2}\right)\cos \phi-1$,

 $\tan (2\pi-\theta)>0$

  and $-1 < \sin \theta < -\frac{-\sqrt{3}}{2}$ then , $\phi$ cannot satisfy 

Answer:

Explanation:

Concept lnvolved. It is based on range of sin x i.e., [-1,1] and the internal for a< x< b.

 Description  of situation As $\theta, \phi \epsilon [0,2\pi]$ and

  $\tan (2 \pi-\theta) 0,-1<\sin \theta <-\frac{\sqrt{3}}{2}$

 $\tan (2 \pi-\theta) >0$ $\Rightarrow$  $-\tan \theta >0$

 $\therefore$  $\theta \epsilon$ II or IV quadrant

 also, $-1 < \sin \theta < -\frac{\sqrt{3}}{2}$

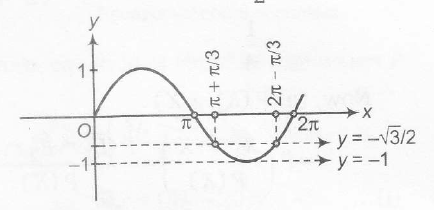
 $\Rightarrow$   $\frac{4 \pi}{3} < \theta < \frac{5 \pi}{3}$ but $\theta \epsilon$ II or IV  quadrant 

 $\Rightarrow$    $\frac{3 \pi}{2} < \theta < \frac{5 \pi}{3}$ .....(i)

 Sol. here

 $2 \cos \theta (1-\sin \phi )$

                       =$\sin^{2} \theta (\tan \frac{ \theta}{2}+\cot \frac{\theta}{2}) \cos \phi-1$

 $\Rightarrow$  $2 \cos \theta-2 \cos \theta \sin  \phi$

  = $\sin^{2} \theta\left(\frac{\sin^{2}\frac{\theta}{2}+\cos^{2} \frac{\theta}{2}}{\sin \frac{\theta}{2} \cos \frac{\theta}{2}}\right) \cos \phi-1$

 =$2 \cos \theta-2 cos \theta \sin \phi$

                              =$2\sin^{2} \theta\left(\frac{1}{\sin\theta}\right) \cos \phi-1$

 =$2 \cos \theta +1=2 \sin \phi \cos \theta+2 \sin \theta \cos \phi$

         $\Rightarrow$  $2 \cos \theta+1=2 \sin ( \theta+\phi)$.....................(ii)

 From Eq.(i)

   $\frac{3 \pi}{2} < \theta < \frac{5 \pi}{3}$ $\Rightarrow 2 \cos \theta+1 \epsilon(1,2)$

  $\therefore$   $1 < \sin (\theta+\phi)<2$

$\rightarrow$   $\frac{1}{2} < \sin (\theta +\phi) <1$......(iii)

 $\Rightarrow$  $\frac{\pi}{6} < \theta +\phi < \frac{5 \pi}{6}$ or $\frac{13 \pi}{6} < \theta +\phi < \frac{17 \pi}{6}$

 $\therefore$  $\frac{\pi}{6} -\theta < \phi < \frac{5 \pi}{6}- \theta$

 or $\frac{13 \pi}{6}-\theta < \phi  < \left(\frac{17 \pi}{6}\right)-\theta$

 $\Rightarrow$ $\phi \epsilon\left(-\frac{3  \pi}{2},-\frac{2\pi}{3}\right)or \left(\frac{2\pi}{3},\frac{7 \pi}{6}\right),$

as $\theta \epsilon\left(\frac{3  \pi}{2},\frac{5 \pi}{3}\right)$

A ship is fitted with with three engines $E_{1},E_{2}$ and $E_{3}$. The engines function independently of each other with respective probabilities 1/2,1/4 and 1/4. For the ship to be operational at least two of its engines must function. Let X denote the event that the ship is operational and let $X_{1},X_{2}$ and $X_{3}$ denotes,respectively the  events that engines $E_{1},E_{2}$ and $E_{3}$ are functioning .Which of the following is/are true?

Answer:

Explanation:

Concept involved It is based on the law of total probability and Bay's Law.

Description of Situation It is given that
ship would work if at least two of engineers must work. If X be an event that the ship works.

 Then  $X \Rightarrow$ either any two of $E_{1},E_{2},E_{3}$ works

or all three engines $E_{1},E_{2},E_{3}$ works 

 Sol. Given  $P(E_{1})=\frac{1}{2},P(E_{2})=\frac{1}{4},P(E_{3})=\frac{1}{4}$

$\therefore$ 

$P(X)=$

$\left\{P(E_{1}\cap E_{2}\cap \overline{E_{3}})+P(E_{1}\cap \overline{E_{2}}\cap E_{3}) + P(\overline{E_{1}}\cap E_{2}\cap E_{3})+P(E_{1}\cap E_{2}\cap E_{3})\right\}$

 =$\left(\frac{1}{2}.\frac{1}{4}.\frac{3}{4}+\frac{1}{2}.\frac{3}{4}.\frac{1}{4}+\frac{1}{2}.\frac{1}{4}.\frac{1}{4}\right)+\left(\frac{1}{2}.\frac{1}{4}.\frac{1}{4}\right)$

    =$\frac{1}{4}$

 Now,  (a)  $P(X_{1}^{c}/X)$

 $=P\left(\frac{X_{1}^{c}\cap X}{P(X)}\right)=\frac{P(\overline {E_{1}} \cap E_{2}\cap E_{3})}{P(X)}$

 $=\frac{\frac{1}{2}.\frac{1}{4}.\frac{1}{4}}{\frac{1}{4}}=\frac{1}{8}$

(b)  

P (Exactly two engines of the ship are functioning)

 $=\frac{P(E_{1}\cap E_{2}\cap\overline{E_{3}})+P(E_{1}\cap \overline{E_{2}}\cap E_{3})+P(\overline{E_{1}}\cap E_{2}\cap E_{3})}{P(X)}$

=$\frac{\frac{1}{2}.\frac{1}{4}.\frac{3}{4}+\frac{1}{2}.\frac{3}{4}.\frac{1}{4}+\frac{1}{2}.\frac{1}{4}.\frac{1}{4}}{\frac{1}{4}}=\frac{7}{8}$

(c) $P\left(\frac{X}{X_{2}}\right)=\frac{P(X \cap X_{2})}{P(X_{2})}$

=P( ship is operating with $E_{2}$ function )/ $P{X_{2}}$

 =$\frac{P(E_{1}\cap E_{2}\cap\overline{E_{3}})+P(\overline{E_{1}}\cap E_{2}\cap{E_{3}})+P(E_{1}\cap E_{2}\cap{E_{3}})}{P(E_{2})}$

$=\frac{\frac{1}{2}.\frac{1}{4}.\frac{3}{4}+\frac{1}{2}.\frac{1}{4}.\frac{1}{4}+\frac{1}{2}.\frac{1}{4}.\frac{1}{4}}{\frac{1}{4}}=\frac{5}{8}$

(d)   $P(X/X_{1})=\frac{P(X\cap X_{1})}{P(X_{1})}$

$=\frac{\frac{1}{2}.\frac{1}{4}.\frac{1}{4}+\frac{1}{2}.\frac{3}{4}.\frac{1}{4}+\frac{1}{2}.\frac{1}{4}.\frac{3}{4}}{\frac{1}{4}}=\frac{7}{16}$

 If y(x) satisfies the differential equation $y'-y \tan x=2 x \sec x$ and y(0)  , then 

Answer:

Explanation:

Concept lnvolved. Linear differential equation under one variable.

 $\frac{dy}{dx}+Py=Q$  ; $IF=e^{\int P dx}$

 $\therefore$    Solution is  , $y(IF)= \int Q. (IF) dx+C$

Sol. $y'- y \tan x=2x \sec x$ and y(0)=0$

 $\Rightarrow$ $\frac{dy}{dx}-y \tan x=2 x \sec x$

 $\therefore$     $IF= \int e^{-\tan x} dx=e^{\log |\cos x|}=\cos x$

 Solution is 

  $y. \cos x=\int 2x.\sec x.\cos x dx+C$

 $\Rightarrow$   $y. \cos x=x^{2}+C$

 As   y(0)=0$\Rightarrow$ C=0

 $\therefore$   $y=x^{2}\sec x$

 Now, $y\left(\frac{\pi}{4}\right)=\frac{\pi^{2}}{8\sqrt{2}}$

$\Rightarrow$  $y'\left(\frac{\pi}{4}\right)=\frac{\pi^{}}{\sqrt{2}}+\frac{\pi^{2}}{8\sqrt{2}}$

$\Rightarrow$  $y\left(\frac{\pi}{3}\right)=\frac{2\pi^{2}}{9}$

$\Rightarrow$  $y'\left(\frac{\pi}{3}\right)=\frac{4 \pi}{3}+\frac{2 \pi^{2}}{3\sqrt{3}}$

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics