JEE 2012 :: General Questions :: Mathematics

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics

The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is

Answer:

Explanation:

The concept involved the Distribution of objects into groups. Here, the student should be particular about objects and groups. i.e.,

Objects                Groups

Distinct                Distinct

Identical              Identical

Distinct               Identical

Identical              Distinct

Description of Situation Here, 5 distinct balls are distributed amongst 3 persons so that each gets at least one ball.

i.e, Distinct $\rightarrow$ Distinct

so, we should make cases

 Case  I            A B C

                       1 1 3

Case II             A B C

                        1 2 2

 sol. number of ways to distribute 5 balls is

$\left(^{5}C_{1}.^{4}C_{3}.^{3}C_{3} \times \frac{3!}{2!}\right)+\left(^{5}C_{1}.^{4}C_{2}.^{2}C_{2} \times \frac{3!}{2!}\right)$

  =60+90

   =150

Let  $f(x)=\begin{cases}x^{2}|\cos \frac{\pi}{x}, & x \neq 0\\0 ,& x = 0\end{cases}$ then f is 

Answer:

Explanation:

Concept Involved To check differentiability at a point we use RHD and LHD at a point and if RHD = LHD, then f(x) is differentiable at the point.

 Description of Situation

 As,   R

$\left\{f'(x)\right\}=\lim_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}$

and   $L\left\{f'(x)\right\}=\lim_{h \rightarrow 0}\frac{f(x-h)-f(x)}{-h}$

 Here, students generaliy gets confused in defining modulus

 Sol. To check differentiable at x=0

  $R\left\{f'(0)\right\}=\lim_{h \rightarrow 0}\frac{f(0+h)-f(0)}{h}$

$=\lim_{h \rightarrow 0}\frac{h^{2}|\cos \frac{\pi}{h}|-0}{h}$

$=\lim_{h \rightarrow 0}h.|\cos \frac{\pi}{h}|=0$

 $L\left\{f'(0)\right\}=\lim_{h \rightarrow 0}\frac{f(0-h)-f(0)}{-h}$

$=\lim_{h \rightarrow 0}\frac{h^{2}|\cos \left(-\frac{\pi}{h}\right)|-0}{-h}}$

         =0

 so, f(x) is differentiable  at x=0

To check differentiability at x=2

$R\left\{f'(2)\right\}=\lim_{h \rightarrow 0}\frac{f(2+h)-f(2)}{h}$

   $=\lim_{h \rightarrow 0}\frac{(2+h)^{2}| \cos \left(\frac{\pi}{2+h}\right)|-0}{h}$

$=\lim_{h \rightarrow 0}\frac{(2+h)^{2} \sin  \left(\frac{\pi}{2}-\frac{\pi}{2+h}\right)}{h}$

$=\lim_{h \rightarrow 0}\frac{(2+h)^{2} \sin  \left(\frac{\pi h}{2(2+h)}\right)}{h.\frac{\pi}{2(2+h)}}$

                                         .$\frac{\pi}{2(2+h)}$

$\Rightarrow$   $R(f'(2))=\pi$

  $L(f'(2))=\lim_{h \rightarrow 0}\frac{f(2-h)-f(2)}{-h}$

  =$\lim_{h \rightarrow 0}\frac{(2-h)^{2}.|\cos \frac{\pi}{2-h}|-2^{2}.|\cos \frac{\pi}{2}|}{-h}$

=$\lim_{h \rightarrow 0}\frac{(2-h)^{2}-\left(-\cos \frac{\pi}{2-h}\right)-0}{-h}$

=$\lim_{h \rightarrow 0}\frac{-(2-h)^{2}.\sin\left( \frac{\pi}{2}-\frac{\pi}{2-h}\right)}{h}$

$\lim_{h \rightarrow 0}\frac{(2-h)^{2}.\sin\left( -\frac{\pi h}{2(2-h)}\right)}{h \times \frac{-\pi}{2(2-h)}}$   

                                             $\times \frac{-\pi}{2(2-h)}$

 $\Rightarrow$    $L.F'(2))=-\pi$

 Thus,  f(x) is differentiable  at x=0 but not at x=2

Let z be a complex number such that the imaginary part of z is non-zero and $a=z^{2}+z+1$  is real. Then, a cannot take the value

Answer:

Explanation:

 Concept involved if $ax^{2}+bx+c=0$ has roots $\alpha, \beta$ , then

 $\alpha, \beta=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$

 for roots to be real $b^{2}-4ac \geq 0$

 Description of Situation As imaginary

part of z=x+iy is non zero

 $\Rightarrow$    $y \neq 0$

 sol. 1 method let z=x+iy

 $\therefore$  $a=(x+iy)^{2}+(x+iy)+1$

$\Rightarrow$  $(x^{2}-y^{2}+x+1-a)+i(2xy+y)=0$

 $\Rightarrow$  $(x^{2}-y^{2}+x+1-a)+iy(2x+1)=0$......(i)

 It is purely real .If ,y(2x+1)=0

 but imagonary part of z, i.em y is non zero

 $\Rightarrow$  2x+1=0 or x= $-\frac{1}{2}$

$\therefore$  From Eq.(i) $\frac{1}{4}-y^{2}-\frac{1}{2}+1-a=0$

 $\Rightarrow$  $a=-y^{2}+\frac{3}{4} \Rightarrow a <\frac{3}{4}$

 II method  Here, $z^{2}+z+(1-a)=0$

 $\therefore$    $z=\frac{-1\pm\sqrt{1-4(1-a)}}{2\times1}$

  $\Rightarrow$  $z=\frac{-1\pm\sqrt{4a-3}}{2}$

 for    z do not have real roots.

  4a-3<0 $\Rightarrow$  a < $\frac{3}{4}$

The integral  $\int  \frac{\sec^{2}x}{(\sec x+\tan x)^{9/2}}dx$ equals to (for some arbitrary constant K)

Answer:

Explanation:

Concept involved Integration by Substitution

i.e,    $I=\int f(g(x)).g'(x) dx $

 put    , g(x)=t $\Rightarrow$ g'(x)dx=dt$

 $\therefore$  $l=\int f(t) dt$

 Description of Situation Generally,

students gets confused after substitution i.e.,

 $\sec x+\tan x=t$

 Now, for sec x  we should use

 $\sec^{2}x-tan^{2}x=1$

 $\Rightarrow$   $(\sec x-\tan x)(\sec x+\tan x)=1$

 $\Rightarrow$  $\sec x-\tan x=\frac{1}{t}$

 sol. Here, $\int  \frac{\sec^{2}x}{(\sec x+\tan x)^{9/2}}dx$

 Put,                           $\sec x+\tan x=t$

 $\Rightarrow$  $(\sec x \tan x+\sec^{2}x) dx=dt$

$\Rightarrow$   $\sec x .t dx=dt$

$\Rightarrow$   $\sec x dx= \frac{dt}{t}$

 $\therefore$  $\sec x-\tan x= \frac{1}{t}$

 $\Rightarrow$  $\sec x=\frac{1}{2}\left(t+\frac{1}{t}\right)$

 $\therefore$   $l=\int \frac{\sec x.\sec x dx}{(\sec x+\tan x)^{9/2}}$

 $\Rightarrow$   $l=\int \frac{\frac{1}{2}\left(t+\frac{1}{t}\right).\frac{dt}{t}}{t^{9/2}}$

$=\frac{1}{2}\int\left(\frac{1}{t^{9/2}}+\frac{1}{t^{13/2}}\right)dt$

 =$-\frac{1}{2}\left\{\frac{2}{7 t^{7/2}}+\frac{2}{11t^{11/2}}\right\}+K$

 =$-\left[\frac{1}{7(\sec x+\tan x)^{1/2}}+\frac{1}{11(\sec x+\tan x)^{11/2}}\right]+K$

$=\frac{-1}{(\sec x+\tan x)^{11/2}}$

       $\left\{\frac{1}{11}+\frac{1}{7}(\sec x+\tan x)^{2}\right\}+K$

The point P is the intersection of the straight line joining the points Q(2,3,5) and R(1,-1,4)  with the plane 5x-4y-z=1.

If S is the foot of the 4. perpendicular drawn from the point T(2,1,4) to QR , then the length of the line segment PS is 

Answer:

Explanation:

Concept Involved

 It is based on two concepts one is the intersection of straight line
and plane and other is the foot of the perpendicular from a point to the straight
line.

 Description of situation

 (i) if the straight line

   $\frac{x-x_{1}}{a}-\frac{y-y_{1}}{b}$

                 =$\frac{z-z_{1}}{c}=\lambda$

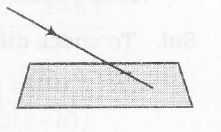
 intersect the plane  Ax+By+Cz+d=0

 Then , $(a \lambda+x_{1},b \lambda+y_{1},c \lambda+z_{1})$ would satisfy

  Ax+By+Cz+d=0

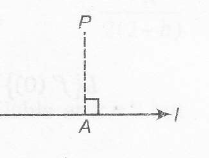
 (ii) If A is the foot of perpendicular from P  to l.

 Then, (dr's of PA) is perpendicular to dr's of l.

$\Rightarrow$ $\overline{PA}.l=0$

Sol. Equation of straight line QR, is 

 $\frac{x-2}{1-2}=\frac{y-3}{-1-3}=\frac{z-5}{4-5}$

 or    $\frac{x-2}{-1}=\frac{y-3}{-4}=\frac{z-5}{-1}$

or $\frac{x-2}{1}=\frac{y-3}{4}=\frac{z-5}{1}=\lambda$

 or $\frac{x-2}{1}=\frac{y-3}{4}=\frac{z-5}{1}=\lambda$ ..........(i)

 $\therefore$   $P(\lambda+2,4\lambda+3,\lambda+5)$ must lie on 5x-4y-z=1

 $\Rightarrow$  $5(\lambda+2)-4(4\lambda+3)-(\lambda+5)=1$

$\Rightarrow$  $5 \lambda+10-16 \lambda-12-\lambda-5=1$

 $\Rightarrow$  $-7-12\lambda=1$

$\lambda=\frac{-2}{3}$ or $P\left(\frac{4}{3},\frac{1}{3},\frac{13}{3}\right)$.......(ii)

Again we assume S from (i) as $S(\mu +2,4\mu + 3, \mu + 5)$

dr's of TS = $(\mu+2-2, 4\mu + 3-1, \mu + 5-4 )$

$(\mu, 4\mu+2, \mu + 1)$

and dr's of QR =(1,4,1)

 since, perpendicular 

$\because$   $1(\mu)+4(4 \mu+2)+1(\mu+1)=0$

 $\Rightarrow$  $\mu=-\frac{1}{2}$ and $S(\frac{3}{2},1,\frac{9}{2})$...(iii)

 $\therefore$  Length of 

 PS= $\sqrt{\left(\frac{3}{2}-\frac{4}{3}\right)^{2}+\left(1-\frac{1}{3}\right)^{2}+\left(\frac{9}{2}-\frac{13}{3}\right)^{2}}$

   $=\frac{1}{\sqrt{2}}$

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics