JEE 2012 :: General Questions :: Mathematics

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics

If a, b, and c are unit vectors satisfying  $|a-b|^{2}+|b-c|^{2}+|c-a|^{2}=9$ then |2a+5b+5c| is 

Answer:

Explanation:

Concept involved if a,b,c are any three vectors

 then$ |a+b+c|^{2} \geq 0$

 $\Rightarrow$    $|a|^{2}+|b|^{2}+|c|^{2}+2(a.b+b.c+c.a) \geq 0$

 $\therefore$    $a.b+b.c+c.a \geq \frac{-1}{2} (|a|^{2}+|b|^{2}+|c|^{2})$

 Sol.Given   $|a-b|^{2}+|b-c|^{2}+|c-a|^{2}=9$

 $\Rightarrow$   $|a|^{2}+|b|^{2}-2a.b+|b|^{2}+|c|^{2}-2b.c+|c|^{2}+|a|^{2}-2c.a=9$

$\Rightarrow$   $6-2(a.b+b.c+c.a)=9$    $( \because  |a|=|b|=|c|=1)$

 $\Rightarrow$    a.b+b.c+c.a=-$\frac{3}{2}$....(i)

 Also, a.b+b.c+c.a  $\geq  \frac{-1}{2} (|a|^{2}+|b|^{2}+|c|^{2}) \geq -\frac{3}{2}$....(ii)

From eq.(i) and (ii)  , we get

|a+b+c|=0

as a.b+b.c+c.a is minimum when |a+b+c|=0

 $\Rightarrow$    a+b+c=0

 $\therefore$   |2a+5b+5c|=|2a+5(b+c)|=|2a-5b|=3

The value of $6+\log_{3/2}$ $\left(\frac{1}{3\sqrt{2}}\sqrt{4-\frac{1}{3\sqrt{2}}\sqrt{4-\frac{1}{3\sqrt{2}}\sqrt{4-\frac{1}{3\sqrt{2}}}}}\right)$ is 

Answer:

Explanation:

Concept involved 

 use of infinite series

 i.e  if y=$\sqrt{x\sqrt{x\sqrt{x....\infty}}}\Rightarrow y=\sqrt{xy}$

 sol.

$6+\log_{3/2}$

$\left(\frac{1}{3\sqrt{2}}\sqrt{4-\frac{1}{3\sqrt{2}}\sqrt{4-\frac{1}{3\sqrt{2}}\sqrt{4-\frac{1}{3\sqrt{2}}}}}\right)$

 Let  $\sqrt{4-\frac{1}{3\sqrt{2}}\sqrt{4-\frac{1}{3\sqrt{2}}\sqrt{....}}}= y$

$\therefore$   $y=\sqrt{4-\frac{1}{3\sqrt{2}}}y$

 $\Rightarrow$  $y^{2}+\frac{1}{3\sqrt{2}}y-4=0$

 $\Rightarrow$  $3 \sqrt{2} y^{2}+y-12\sqrt{2}=0$

 $\therefore$   $y=\frac{-1\pm 17}{6\sqrt{2}}$  or  $y=\frac{8}{3\sqrt{2}}$

 Now, 

$6+\log_{3/2}\left(\frac{1}{3\sqrt{2}}.y\right)=6+\log_{3/2}\left(\frac{1}{3\sqrt{2}}.\frac{8}{3\sqrt{2}}\right)$

 =$6+\log_{3/2} \left(\frac{4}{9}\right)=6+\log _{3/2}\left(\frac{3}{2}\right)^{-2}$

=$6-2\log_{3/2} \left(\frac{3}{2}\right)=4$

Let $f:R \rightarrow R$ be defined as $f(x)=|x|+|x^{2}-1|$ The total number  of points at which f attains either a local maximum or  a local minimum is 

Answer:

Explanation:

Concept involved
(i) Local maximum and local minimum are those points at which f'(x)=0 when, defined for all real numbers.
(ii) Local maximum and local minimum for piecewise function are also been checked at sharp edges

Descriotion of Situation

   $y=|x|=\begin{cases}x, & x \geq 0\\-x, & x < 0\end{cases}$

also,  $y=|x^{2}-1|=\begin{cases}(x^{2}-1), & x \leq-1 or x\geq1\\(1-x^{2}), & -1\leq x \leq 1\end{cases}$

 sol. $y=|x|+|x^{2}-1|$

=$\begin{cases}-x^{2}-x+1, & x \leq -1\\-x^{2}-x+1, & -1\leq x \leq 0 \\ -x^{2}+x+1, &0\leq x\leq1\\x^{2}+x-1 &x\geq1\end{cases}$

which could be graphically shown as

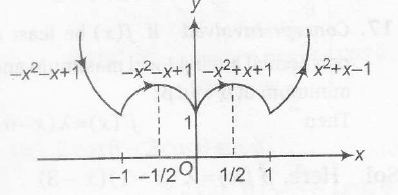
Thus, f (x) attains maximum at

 $x=\frac{1}{2},\frac{-1}{2}$ and f(x) attains minimum at x=-1,0,1

 $\Rightarrow$  Total number of points=5

Let p(x) be a  be a real polynomial of least degree which has a local maximum at x = 1 and a local minimum at x=3. If p(1)=6 and P(3)=2 , the p '(0) is 

Answer:

Explanation:

Concept lnvolved If f(x) be least degree polynomial having local maximum and local
minimum at $\alpha$ and $\beta$

 Then   $f'(x)=\lambda (x-\alpha)(x-\beta)$

 Sol.Here $p'(x)=\lambda(x-1)(x-3)$

  =$\lambda(x^{2}-4x+3)$

Integrating both sides between 1 to 3

 $\int_{1}^{3}p'(x) dx=\int_{1}^{3}\lambda(x^{2}-4x+3)dx  $

$\Rightarrow$    $(p(x))_{1}^{3}=\lambda\left(\frac{x^{3}}{3}-2x^{2}+3x\right)_{1}^{3}$

 $\Rightarrow$   P(3)-p(1)

    =$ \lambda \left((9-18+9)-\left(\frac{1}{3}-2+3)\right)\right)$

$2-6=\lambda\left\{\frac{-4}{3}\right\}$

$\therefore$  $p'(x)=3(x-1)(x-3)$

$\therefore$  $p'(0)=9$

Let S be the focus of the parabola $y^{2}=8x$ and let PQ be the common chord of the circle  $x^{2}+y^{2}-2x-4y=0$ and the given parabola.The area of the $\triangle OPS$ is 

Answer:

Explanation:

Concept Involved Parametric coordinates for $y^{2} = 4ax$ are$ (at^{2},2at).$

Description of Situation As the circle intersects the parabola at P and Q. Thus points P and Q should satisfy the circle.

Sol. $p(2t^{2},4t)$ sholud lie on

 $x^{2}+y^{2}-2x-4y=0$

 $\Rightarrow$  $4t^{4}+16t^{2}-4t^{2}-16 T-0$

 $\Rightarrow$  $4t^{4}+12t^{2}-16t=0$

 $\Rightarrow$ $4t{(t^{3}+3t-4)}=0$

 $\Rightarrow$  $4t(t-1)(t^{2}+t+4)=0$

 $\therefore$  $t=0,1 \Rightarrow P(2,4)$

 Thus, are of $\triangle OPs=\frac{1}{2} OS \times PQ$

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics