Answer:
Option A,C,D
Explanation:
Concept lnvolved. It is based on range of sin x i.e., [-1,1] and the internal for a< x< b.
Description of situation As θ,ϕϵ[0,2π] and
tan(2π−θ)0,−1<sinθ<−√32
tan(2π−θ)>0 ⇒ −tanθ>0
∴ θϵ II or IV quadrant
also, −1<sinθ<−√32
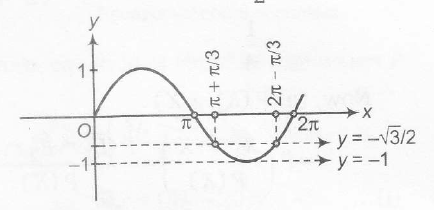
⇒ 4π3<θ<5π3 but θϵ II or IV quadrant
⇒ 3π2<θ<5π3 .....(i)
Sol. here
2cosθ(1−sinϕ)
=sin2θ(tanθ2+cotθ2)cosϕ−1
⇒ 2cosθ−2cosθsinϕ
= sin2θ(sin2θ2+cos2θ2sinθ2cosθ2)cosϕ−1
=2cosθ−2cosθsinϕ
=2sin2θ(1sinθ)cosϕ−1
=2cosθ+1=2sinϕcosθ+2sinθcosϕ
⇒ 2cosθ+1=2sin(θ+ϕ).....................(ii)
From Eq.(i)
3π2<θ<5π3 ⇒2cosθ+1ϵ(1,2)
∴ 1<sin(θ+ϕ)<2
→ 12<sin(θ+ϕ)<1......(iii)
⇒ π6<θ+ϕ<5π6 or 13π6<θ+ϕ<17π6
∴ π6−θ<ϕ<5π6−θ
or 13π6−θ<ϕ<(17π6)−θ
⇒ ϕϵ(−3π2,−2π3)or(2π3,7π6),
as θϵ(3π2,5π3)