Answer:
Option A,B
Explanation:
Concept lnvolved
Equation of tangent to $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ is
$y= mx \pm \sqrt{a^{2}m^{2}-b^{2}}$
Description of Situation If two straight
lines
$a_{1}x+b_{1}y+c_{1}=0$
and $ax_{2}+b_{2}y+c_{2}=0$ are identical
$\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$
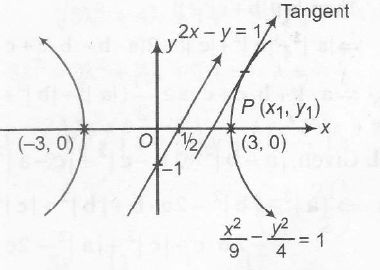
sol., Equation of tangent , parallel to
y=2x-1
$\Rightarrow$ $y=2x\pm\sqrt{9(4)-4}$
$\therefore$ $y =2x \pm \sqrt{32}$....(i)
The equation of tangent at $(x_{1},y_{1})$ is
$\frac{xx_{1}}{9}-\frac{yy_{1}}{4}=1$ ...(ii)
from Eqs(i) and (ii) , we get
$\frac{2}{\frac{x_{1}}{9}}=\frac{-1}{\frac{-y_{1}}{4}}=\frac{\pm\sqrt{32}}{1}$
$\Rightarrow$ $x_{1}=-\frac{9}{2\sqrt{2}} and y_{1}=-\frac{1}{\sqrt{2}}$
or $x_{1}=\frac{9}{2\sqrt{2}}$ and $ y_{1}=\frac{1}{\sqrt{2}}$
