Discussion Forum

Let S be the focus of the parabola $y^{2}=8x$ and let PQ be the common chord of the circle  $x^{2}+y^{2}-2x-4y=0$ and the given parabola.The area of the $\triangle OPS$ is 

Answer:

Explanation:

Concept Involved Parametric coordinates for $y^{2} = 4ax$ are$ (at^{2},2at).$

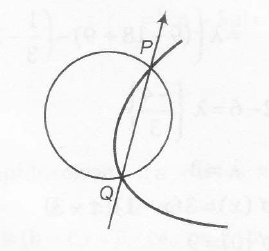
Description of Situation As the circle intersects the parabola at P and Q. Thus points P and Q should satisfy the circle.

Sol. $p(2t^{2},4t)$ sholud lie on

 $x^{2}+y^{2}-2x-4y=0$

 $\Rightarrow$  $4t^{4}+16t^{2}-4t^{2}-16 T-0$

 $\Rightarrow$  $4t^{4}+12t^{2}-16t=0$

 $\Rightarrow$ $4t{(t^{3}+3t-4)}=0$

 $\Rightarrow$  $4t(t-1)(t^{2}+t+4)=0$

 $\therefore$  $t=0,1 \Rightarrow P(2,4)$

 Thus, are of $\triangle OPs=\frac{1}{2} OS \times PQ$