Discussion Forum

Let $f:R \rightarrow R$ be defined as $f(x)=|x|+|x^{2}-1|$ The total number  of points at which f attains either a local maximum or  a local minimum is 

Answer:

Explanation:

Concept involved
(i) Local maximum and local minimum are those points at which f'(x)=0 when, defined for all real numbers.
(ii) Local maximum and local minimum for piecewise function are also been checked at sharp edges

Descriotion of Situation

   $y=|x|=\begin{cases}x, & x \geq 0\\-x, & x < 0\end{cases}$

also,  $y=|x^{2}-1|=\begin{cases}(x^{2}-1), & x \leq-1 or x\geq1\\(1-x^{2}), & -1\leq x \leq 1\end{cases}$

 sol. $y=|x|+|x^{2}-1|$

=$\begin{cases}-x^{2}-x+1, & x \leq -1\\-x^{2}-x+1, & -1\leq x \leq 0 \\ -x^{2}+x+1, &0\leq x\leq1\\x^{2}+x-1 &x\geq1\end{cases}$

which could be graphically shown as

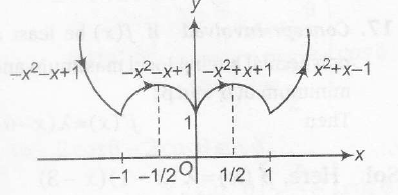
Thus, f (x) attains maximum at

 $x=\frac{1}{2},\frac{-1}{2}$ and f(x) attains minimum at x=-1,0,1

 $\Rightarrow$  Total number of points=5