JEE 2011 :: General Questions :: Mathematics

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics

Match the statements given in Column I with the intervals/union of intervals given in Column II

Answer:

Explanation:

 (A) Given , $|z|=1 \Rightarrow  z. \overline{z}=1$

$\therefore$  $\frac{2iz}{1-z^{2}}=\frac{2iz}{z.\overline{z}-z^{2}}=\frac{2i}{\overline{z}-z},$

Let z=x+iy

 $\therefore$  $z-\overline{z}=2iy= \frac{2i}{-2iy}=-\frac{1}{y}$ .......(i)

 where, $y=\sqrt{1-x^{2}}$

 $\therefore$   $-1\leq y\leq1 \Rightarrow -1 \leq y$

 and $y\leq 1 \Rightarrow-1 \geq \frac{1}{y}$   and  $\frac{1}{y}\geq 1$

 $\Rightarrow$  $Re\left(\frac{2iz}{1-z^{2}}\right)\epsilon (-\infty ,-1)\cup[1, \infty)$

 (B) $f(x)= \sin^{-1}\left(\frac{8(3^{x-2})}{1-3^{2(x-1)}}\right)$,

 For domain, $-1\leq \frac{8(3^{x-2})}{1-3^{2(x-1)}}\leq1$

 $\Rightarrow$  $-1\leq \frac{9.(3^{x-2})-(3^{x-2})}{1-3^{2(x-1)}}\leq1$

 $\therefore$    $-1\leq \frac{3^{x}-3^{x-2}}{1-3^{x}. 3^{(x-2)}}\leq1$

       $ \frac{3^{x}-3^{x-2}}{1-3^{x}. 3^{(x-2)}}\geq -1$

 $\Rightarrow$   $ \frac{(3^{x}-1)(3^{x-2}-1)}{(3^{x+1}+1). 3^{x-1}-1}\geq 0$

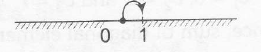
 $\Rightarrow$   $x\epsilon (-\infty,0] \cup [1, \infty)$

 and   $\frac{3^{x}-3^{x-2}}{1-3^{x}.3^{x-2}}\leq 1$

 $\Rightarrow$   $\frac{(3^{x-2}-1)(3^{x}+1)}{(3^{x-1}+1).(3^{x-1}-1)}\geq 0$

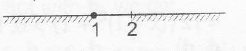
and    $x \epsilon (-\infty,1) \cup [2, \infty)$

 $\therefore$  $x \epsilon (-\infty,0] \cup [2, \infty)$

(C)  $f(\theta)=\begin{bmatrix}1 & \tan \theta&1 \\- \tan \theta & 1& \tan \theta\\ -1& -\tan \theta &1 \end{bmatrix}$

   $R_{1} \rightarrow R_{1}+R_{3}$

$f(\theta)=\begin{bmatrix}0 &0 &2 \\- \tan \theta & 1& \tan \theta\\ -1& -\tan \theta &1 \end{bmatrix}$

=  $2(\tan^{2} \theta+1)=2 \sec^{2} \theta \geq 2$

 $f(\theta) \epsilon [2, \infty)$

(D)  $f(x)=x^{3/2}(3x-10);x \geq 0$

 $f'(x)=x^{3/2}.3+\frac{3}{2}.x^{1/2}(3x-10)$

    $=3x^{1/2}\left\{x+\frac{1}{2}(3x-10)\right\}$

   $=\frac{3}{2}x^{1/2}\left\{2x+3x-10\right\}$

  $=\frac{15}{2}x^{1/2}(x-2)$

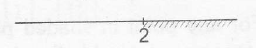
 $\therefore$   $x\geq 2$

Match the statements given in Column I with the values given in column II

Answer:

Explanation:

(A)  $\therefore$  $|a|=\sqrt{1+3}=2$

                             $|b|= \sqrt{1+3}=2$

                            $ |c|=\sqrt{12}=2 \sqrt{3}$

 Using Cosine law, 

 $\cos C= \frac{|a|^{2}+|b|^{2}-|c|^{2}}{2|a||b|}$

 =  $\frac{4+4-12}{2 \times 2 \times 2}=\frac{-4}{8}=\frac{-1}{2}$

 $\Rightarrow$  $\angle C=120^{0}= \frac{2 \pi}{3}$

(B) $\int_{a}^{b} f(x) dx-3\left(\frac{x^{2}}{2}\right)_{a}^{b}=(a^{2}-b^{2})$

$\Rightarrow \int_{a}^{b} f(x) dx-\frac{3}{2}(b^{2}-a^{2})=(a^{2}-b^{2})$

$\Rightarrow \int_{a}^{b} f(x) dx=(a^{2}-b^{2})+\frac{3}{2}(b^{2}-a^{2})$

  = $\frac{b^{2}-a^{2}}{2}$

 $\Rightarrow$  $\Rightarrow \int_{a}^{b} f(x) dx=\frac{b^{2}-a^{2}}{2}$

   $f(x)=x \Rightarrow  f(\frac{\pi}{6})=\frac{\pi}{6}$

 (C) $\frac{\pi^{2}}{\log_{e}3}\int_{7/6}^{5/6} \sec(\pi x) dx$

$\Rightarrow\frac{\pi^{2}}{\log_{e}3}\left\{\frac{\log|\sec \pi x+\tan \pi x|}{\pi}\right\}_{7/6}^{5/6}$

 $\Rightarrow\frac{\pi}{\log 3}\left\{ \log |\sec \frac{5 \pi}{6}+\tan \frac{5 \pi}{6}|-\log | \sec \frac{7 \pi}{6}+\tan \frac{7 \pi}{6}|\right\}$

 $\Rightarrow$  $\frac{\pi}{\log 3}\left\{ \log |\sqrt{3}|-\log |\frac{1}{\sqrt{3}}|\right\}$

 $\Rightarrow$ $\frac{\pi}{\log 3} { \log 3}= \pi$

(D) $|arg \frac{1}{(1-z)}|, for |z|=1$

 $\Rightarrow$   $|arg (1-z)^{-1}|$

 $\Rightarrow$  $|- arg (1-z)| \Rightarrow |arg (1-z)|$

 from Figure , arg (z-1) is maximum = $\pi$

The straight line 2x - 3y = 1 divides the circular region $x^{2}+y^{2}\leq 6$ into two  parts  .If  $S=\left\{\left(2,\frac{3}{4}\right),\left(\frac{5}{2},\frac{3}{4}\right),\left(\frac{1}{4},-\frac{1}{4}\right),\left(\frac{1}{8},\frac{1}{4}\right)\right\}$, then the  number of point(s) in S lying inside the smaller part is 

Answer:

Explanation:

$x^{2}+y^{2} \leq 6$  and 2x-3y=1 is shown as,

For the point to lie in the shaded part, origin and the point lie on opposite side
of straight line L.

 $\therefore$ For any point in shaded part L >0

 and for any point inside the circle S <0

 Now, for $\left(2,\frac{3}{4}\right) L:2x-3y-1$

 $L:4-\frac{9}{4}-1 =\frac{3}{4} >0$

 and   $S:x^{2}+y^{2}-6,$

 $S:4+ \frac{9}{16} -6<0$

 $\Rightarrow$   $\left(2,\frac{3}{4}\right)$  lies in shaded part

 For  $\left(\frac{5}{2},\frac{3}{4}\right)L:5-9-1<0$ {neglect}

 For $\left(\frac{1}{4},-\frac{1}{4}\right)L:\frac{1}{2}+\frac{3}{4}-1>0$ }

 $\therefore$ $\left(\frac{1}{4},-\frac{1}{4}\right)$  lies in the shaded part

 For $\left(\frac{1}{8},\frac{1}{4}\right)$L:$\frac{1}{4}-\frac{3}{4}-1 <0$ [neglect]

 $\Rightarrow$   only 2  points lie in the shaded  part 

The number of distinct real roots of $x^{4}-4x^{3}+12x^{2}+x-1=0$

Answer:

Explanation:

$f(x)=x^{4}-4x^{3}+12x^{2}+x-1$

 $f'(x)= 4x^{3}-12x^{2}+24x+1$

 $f''(x)=12x^{2}-24x+24$

 =$12(x^{2}-2x+2)$

=$12(x-1)^{2}+1)>0$, for all x

 $\Rightarrow$ f'(x) is increasing

 Since , f'(x)  is cubic and increasing

 $\Rightarrow$  f'(x) has only one real  root and two imaginary roots

 $\therefore$   f(x) cannot have all distinct root

 $\Rightarrow$  Atmost 2 real roots

 Now,  f(-1)=15

 f(0)=-1 and f(1)=9

 $\therefore$ f(x)   must have one root in (-1,0) and other in (0,1)

 $\Rightarrow$  2 real roots

Let M be a 3 x3 matrix satisfying

$M\begin{bmatrix}0  \\1 \\0 \end{bmatrix}=\begin{bmatrix}-1  \\2 \\3 \end{bmatrix},M\begin{bmatrix}1  \\-1\\0 \end{bmatrix}=\begin{bmatrix}1  \\1 \\-1 \end{bmatrix}$  and  $M\begin{bmatrix}1  \\1 \\1 \end{bmatrix}=\begin{bmatrix}0  \\0 \\12 \end{bmatrix}$

Then, the sum  of the diagonal entries of M is

Answer:

Explanation:

Let $M=\begin{bmatrix}a_{1} & a_{2}&a_{3} \\b_{1} & b_{2}&b_{3}\\c_{1}&c_{2}&c_{3} \end{bmatrix}$

 $\therefore$  $M\begin{bmatrix}0  \\1\\0 \end{bmatrix}=\begin{bmatrix}-1  \\2\\3 \end{bmatrix},M\begin{bmatrix}1  \\-1\\0 \end{bmatrix}=\begin{bmatrix}1  \\1\\-1 \end{bmatrix}$

        $ M\begin{bmatrix}1  \\1\\1 \end{bmatrix}=\begin{bmatrix}0  \\0\\12 \end{bmatrix}$

$\Rightarrow$$ \begin{bmatrix}a_{2}  \\b_{2}\\c_{2} \end{bmatrix}=\begin{bmatrix}-1  \\2\\3 \end{bmatrix},\begin{bmatrix}a_{1}-a_{2}  \\b_{1}-b_{2}\\c_{1}-c_{2} \end{bmatrix}=\begin{bmatrix}1  \\1\\-1 \end{bmatrix}$

$,\begin{bmatrix}a_{1}+a_{2}+a_{3}  \\b_{1}+b_{2}+b_{3}\\c_{1}+c_{2}+c_{3} \end{bmatrix}=\begin{bmatrix}0  \\0\\12 \end{bmatrix}$

 $\Rightarrow$   $a_{2}=-1,b_{2}=2,c_{2}=3,a_{1}-a_{2}=1$, $b_{1}-b_{2}=1,c_{1}-c_{2}=-1$

 $\Rightarrow$   $a_{1}+a_{2}+a_{3}=0,b_{1}+b_{2}+b_{3}=0,$

 $c_{1}+c_{2}+c_{3}=12$

 $\therefore$  $a_{1}=0$ ,$b_{2}=2$ and $c_{3}=7$

Hence, sum of diagonal elements

=0+2+7=9

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics