JEE 2011 :: General Questions :: Mathematics

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics

A straight line L through the point (3, - 2) is inclined at an angle 60° to the line $\sqrt{3} x+y=1$ . If L also intersects the X-axis, there the equation of L is

Answer:

Explanation:

A straight lire passing through P and making an angle of  $\alpha=60^{0}$ is given by

 $\frac{y-y_{1}}{x-x_{1}}= \tan ( \theta \pm \alpha)$

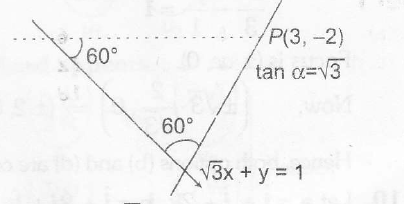
 where  $\sqrt{3}x+y=1$

 $\Rightarrow$  $y=-\sqrt{3}x+1$

 Then , $\tan \theta= -\sqrt{3}$

 $\Rightarrow$  $\frac{y+2}{x-3}=\frac{\tan \theta \pm \tan \alpha}{ 1 \pm \tan \theta \tan \alpha}$

 $\Rightarrow$   $\frac{y+2}{y-3}=\frac{-\sqrt{3}+\sqrt{3}}{1-(-\sqrt{3})(\sqrt{3})}$

 and   $\frac{y+2}{x-3}= \frac{-\sqrt{3}-\sqrt{3}}{1+(-\sqrt{3})(\sqrt{3})}$

 $\Rightarrow$   y+2=0

 and      $\frac{y+2}{x-3}=\frac{-2 \sqrt{3}}{1-3}= \sqrt{3}$

$\Rightarrow$   $y+2= \sqrt{3}x-3 \sqrt{3}$

 Neglecting , y+2=0  as it does not interest Y-axis

Let the straight line x = b divide the area enclosed by   $y=(1-x)^{2},y=0$ and x=0 into two parts $R_{1}(0\leq x\leq b)$and $R_{2}(b\leq x \leq1)$   such that $R_{1}-R_{2}=\frac{1}{4}$

Answer:

Explanation:

Here area between 0 to b is $R_{1}$ and b to 1 is $R_{2}$

$\therefore$  $\int_{0}^{b} (1-x)^{2}dx-\int_{b}^{1} (1-x)^{2}dx=\frac{1}{4}$

$\Rightarrow$  $\left(\frac{(1-x)^{3}}{-3}\right)_{0}^{b}-\left(\frac{(1-x)^{3}}{-3}\right)^{1}_{b}=\frac{1}{4}$

$\Rightarrow$  $-\frac{1}{3}{(1-b)^{3}-1})+\frac{1}{3}(0-(1-b)^{3})=\frac{1}{4}$

$\Rightarrow$   $-\frac{2}{3}(1-b)^{3}=-\frac{1}{3}+\frac{1}{4}=-\frac{1}{12}$

$\Rightarrow$   $(1-b)^{3}=\frac{1}{8}$

$\Rightarrow$   $(1-)=\frac{1}{2} \Rightarrow  b= \frac{1}{2}$

Let  $a= \widehat{i}+\widehat{j}+\widehat{k},b=\widehat{i}-\widehat{j}+\widehat{k}$ ans $c=\widehat{i}-\widehat{j}-\widehat{k}$ be three vectors. A vector v in the plane of a and b whose projection  of c is $\frac{1}{\sqrt{3}}$ is given by 

Answer:

Explanation:

 let  v$a+ \lambda b$

 $v= (1+ \lambda)\widehat{i}+(1-\lambda) \widehat{j}+(1+\lambda)\widehat{k}$

 Projection of v on c= $\frac{1}{\sqrt{3}}$

$\Rightarrow$   $\frac{v.c}{|c|}=\frac{1}{\sqrt{3}}$

$\Rightarrow$ $\frac{(1+\lambda)-(1-\lambda)-(1+\lambda)}{\sqrt{3}} =\frac{1}{\sqrt{3}}$

$\Rightarrow$  $1+ \lambda-1+\lambda-1-\lambda=1$

$\Rightarrow$   $\lambda-1=1 \Rightarrow \lambda=2$

$\therefore$  $v=3 \widehat{i}-\widehat{j}+3 \widehat{k}$

• General Questions - Physics
• General Questions - Chemistry
• General Questions - Mathematics