Answer:
Option B
Explanation:
A straight lire passing through P and making an angle of α=600 is given by
y−y1x−x1=tan(θ±α)
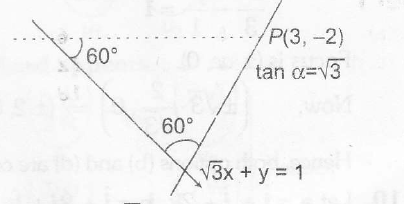
where √3x+y=1
⇒ y=−√3x+1
Then , tanθ=−√3
⇒ y+2x−3=tanθ±tanα1±tanθtanα
⇒ y+2y−3=−√3+√31−(−√3)(√3)
and y+2x−3=−√3−√31+(−√3)(√3)
⇒ y+2=0
and y+2x−3=−2√31−3=√3
⇒ y+2=√3x−3√3
Neglecting , y+2=0 as it does not interest Y-axis