Geomatry is important for may applications. In nature we come across numerous geomatric shapes such as hexagonal snowflakes, cylindrical pies, sperical ball and so on. There were lot of practical implimentaion for geomatry in many fields such as carpentry, architecture, designing, engineering and constructions.
Angle
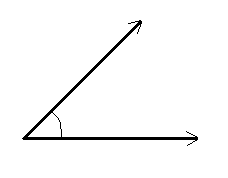
Definition:
An angle is a figure formed by two rays with the same initial point. The common initial point is called the vertex of the angle and the rays are called its arms or sides. Angle measures the ratio of length of a circular arc to its radious. The word angle comes from a latin word angulus, its meamimg "a comer".
Different types of angles
1. Acute angle
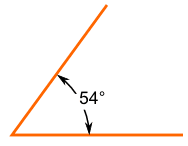
An anlge which is greater than zero but less than a right angle is called acute angle. The meaning of acute is sharp
2. Right angle
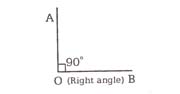
An angle whose measure is exactly equal to 90° is called right angle. Two lines that forms right angle are said to be normal, orthoganol or perpenticular.
3. Obtuse angle
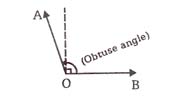
An angle which is greater than right angle and less than 180° is called obtuse angle. The meaning of obtuse is "blunt".
4. Straight angle
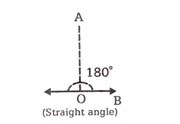
An angle whose measure is exactly 180° is called straight angle.
5. Reflex angle
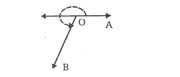
An angle which is greater than 180° and less than 360° is called reflex angle
6. Complete angle

An angle whose measure is 360° is called a complete angle
Types Of Pairs Of angle:
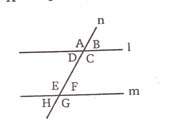
Let 1 and m be two parallel lines, n be a transversal for 1 and m.
Adjacent angles:
Two angles are said to be adjacent, if tbey have a common vertex and a common arm. In the figure, (A,B), (A,D), (C,D)......etc are adjacent angles.
Linear pair:
Two adjacent angles are said to form a linear pair of angles, if their two non-common arm are opposite rays. The sum of measures of angles of the linear pair is 180° . in the figure, (A,B), (A,D), (C,D), (C,B)....etc are linear pair.
Vertically opposite angles:
Two angles formed by two intersecting lines having no common arm are called vertically opposite angles. In the figure, (A,C) (B,D) (E,G) (H,F) are vertically opposite angles. Vertically opposite angles are always equal.
Interior angles:
Angles which are within the parallel lines l,m are called interior angles. In the figure, C, D, E, F are interior angles.
Exterior angles:
Angles which are not within the parallel lines are called exterior angles. In the figure. A, B, H, G are exterior angles.
Corresponding angles :
(A,E), (B,F), (D,H), (C,G) are called corresponding angles. These pair of angles are equal.
Alternate interior angles :
(C,E), (D,F) are alternate interior angles. These pair of alternate interior angles are equal.
Alternate exterior angles:
(B,H), (A,G) are alternate exterior angles. These pair of alternate exterior angles are equal.
Complementary angles :
If the sum of two angles is 90°, then the pair of angles are said to be complementary angles.
Supplementary angles :
If the sum of two angles is 180°, then the pair of angles are said to be supplementary angles.
Take an online aptitude test in examfriend