Answer:
Option B,C
Explanation:
Here, f(x)
$=\lim_{n \rightarrow \infty}\left[\frac{n^{n}(x+n)(x+\frac{n}{2})....(x+\frac{n}{n})}{n!(x^{2}+n^{2})(x^{2}+\frac{n^{2}}{4}).....(x^{2}+\frac{n^{2}}{n^{2}})}\right]^{\frac{x}{n}}$
x>0
Taking log on both sides, we get $\log_{e}[f(x)]$
$ =\lim_{n \rightarrow \infty}\log\left[\frac{n^{n}(x+n)(x+\frac{n}{2})....(x+\frac{n}{n})}{n!(x^{2}+n^{2})(x^{2}+\frac{n^{2}}{4}).....(x^{2}+\frac{n^{2}}{n^{2}})}\right]^{\frac{x}{n}}$
$=\lim_{n \rightarrow \infty}\frac{x}{n}.\log \left[\frac{\prod_{r=1}^{n}(x+\frac{1}{r/n})}{\prod_{r=1}^n(x^{2}+\frac{1}{(r/n)^{2}})\prod_{r=1}^{n}(r/n)}\right]$
$=x\lim_{n \rightarrow \infty}\frac{1}{n}\sum_{r=1}^{n}\log\left[\frac{x+\frac{n}{r}}{(x^{2}+\frac{n^{2}}{r^{2}})(r/n)}\right]$
$=x\lim_{n \rightarrow \infty}\frac{1}{n}\sum_1^n \log \left[\frac{\frac{r}{n}.x+1}{\frac{r^{2}}{n^{2}}.x^{2}+1}\right]$
Converting summation into definite integration, we get $\log_{e}[f(x)]$
$=x\int_{0}^{1} \log (\frac{xt+1}{x^{2}t^{2}+1})dt$
put $tx=z\Rightarrow xdt=dz$
$\therefore \log_{e}[f(x)]=x\int_{0}^{x} \log(\frac{1+z}{1+z^{2}})\frac{dz}{x}$
$\Rightarrow \log_{e}[f(x)]=\int_{0}^{x} \log(\frac{1+z}{1+z^{2}})dz$
Using Newton-Leibnitz formula, we get
$\frac{1}{f(x)}.f'(x)=\log(\frac{1+x}{1+x^{2}})......(i)$
Here x=1,
$\frac{f'(1)}{f(1)}=\log(1)=0$
$\therefore$ F'(1)=0
Now,sign scheme of f'(x) is shown below
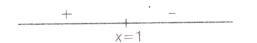
$\therefore$ At x=1, function attains maximum
Since, f(x) increases on (0,1)
f(1)>f(1/2)
$\therefore$ Option (a) is incorrect
f(1/3)<f(2/3)
$\therefore$ Option (b) is correct
Also ,f'(x)<0, when x>1
$\Rightarrow$ f'(2)<0
$\therefore$ Option(c) is correct
Also, $\frac{f'(x)}{f(x)}=\log( \frac{1+x}{1+x^{2}})$
$\therefore$ $\frac{f'(3)}{f(3)}-\frac{f'(2)}{f(2)}=\log(\frac{4}{10})-\log(\frac{3}{5})$
= $\log(2/3)<0$
$\Rightarrow \frac{f'(3)}{f(3)}<\frac{f'(2)}{f(2)}$
$\therefore$ Option (d) is incorrect