Answer:
Option B,C
Explanation:
Let θ be the angle between $\hat{u} $ and $\vec{v} $
$\therefore|\hat{u} \times \overrightarrow{v}|=1\Rightarrow|\hat{u}|\overrightarrow{v}|\sin \theta=1$
$\therefore |\overrightarrow{v}| \sin \theta=1 $ $[\therefore |\hat{u}|=1]$ .......(i)
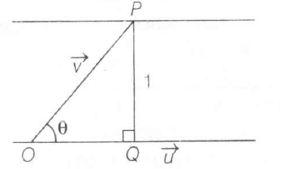
Clearly, there may be infinite vectors
$\overrightarrow{OP}=\overrightarrow{v}$ , such that P is always 1 unit distance from $\hat{u}$.
$\therefore$ Option (b) is correct.
Again, let Φ be the angle between $\hat{w}$ and $\hat{u}\times\overrightarrow{v}.$
$\therefore \hat{w}.(\hat{u}\times\overrightarrow{v})=1\Rightarrow |\hat{w}||\hat{u}\times\overrightarrow{v}|\cos \phi =1$
$\Rightarrow \cos \phi=1\Rightarrow\phi=0$
Thus, $\hat{w}=\hat{u}\times \overrightarrow{v}$
Now, if $\hat{u}$ lies in XY-plane, then
$\begin{vmatrix}\hat{i} & \hat{j}& \hat{k} \\u_{1} & u_{2}&0 \\ v_{1}&v_{2}&v_{3} \end{vmatrix}$
or $\hat{u}=u\hat{i}+u_{2}\hat{j}$
$\therefore\hat{w}=(u_{2}v_{3})\hat{i}-(u_{1}v_{3})\hat{j}+(u_{1}v_{2}-v_{1}u_{2})\hat{k}$
$\therefore\hat{w}=\frac{1}{\sqrt{6}}(\hat{i}+\hat{j}+2\hat{k})$
$\therefore$ $u_{2}v_{3}=\frac{1}{\sqrt{6}}\Rightarrow u_{1}v_{3}=\frac{-1}{\sqrt{6}}$
$\Rightarrow \frac{u_{2}v_{3}}{u_{1}v_{3}}=-1$ or $|u_{1}|=|u_{2}|$
$\therefore$ Option (c) is correct.
Now, if $\hat{u}$ lies un XZ-plane, then $\hat{u}= u_{1}\hat{i}+u_{3}\hat{k}$
$\therefore$
$\begin{vmatrix}\hat{i} & \hat{j}& \hat{k} \\u_{1} & 0&u_{3} \\ v_{1}&v_{2}&v_{3} \end{vmatrix}$
$\Rightarrow w=(-v_{2}u_{3})\hat{i}-(u_{1}v_{3}-u_{3}v_{1})\hat{j}+(u_{1}v_{2})\hat{k}$
$\Rightarrow \hat{w}=\frac{1}{\sqrt{6}}(\hat{i}+\hat{j}+2\hat{k})$
$= -v_{2}u_{3}=\frac{1}{\sqrt{6}}$ and $u_{1}v_{2}=\frac{2}{\sqrt{6}}$
$=|u_{2}|=2|u_{3}|$
$\therefore$ Option (d) is incorrect
