Discussion Forum

Let P be the image of the point (3,1,7) with respect to the plane  x-y+z=3 Then, the equation of the plane passing through P and containing the straight line  $\frac{x}{1}=\frac{y}{2}=\frac{z}{1}$ is

Answer:

Explanation:

Let image of Q(3,1,7) w.r.t

         x-y+z=3 be $P (\alpha,\beta,\gamma)$

               $\therefore  \frac{\alpha-3}{1}=\frac{\beta-1}{-1}=\frac{\gamma-7}{1}$

           $=\frac{-2(3-1+7-3)}{1^{2}+(-1)^{2}+(1)^{2}}$

            $\Rightarrow\alpha-3=1-\beta=\gamma-7=-4$

$\therefore$     $\alpha=-1,\beta=5,\gamma=3$

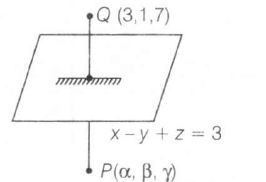
Hence, the image of Q(3,1,7) is P(-1,5,3) .

        to find equation of plane passing through P(-1,5,3) and containing  $\frac{x}{1}=\frac{y}{2}=\frac{z}{1}$

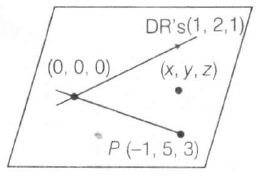
$\Rightarrow$ $\begin{bmatrix}x-1 & y-0 & z-1 \\1-0 & 2-0 &1-0\\-1-0&5-0&3-0 \end{bmatrix}=0$

$\Rightarrow x (6-5)-y(3+1)+z(5+2)=0$

$\therefore$    x-4y+7z=0