JEE 2014 :: Advanced 2014 :: Mathematics 2014

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014

Let f₁:R $\rightarrow$R, f₂:[0,$\infty$] $\rightarrow$ R, f_a : R $\rightarrow$ R

 and f₄:R$\rightarrow$ [0,$\infty$] be defined by

   $f_{1}(x)=\begin{cases}|x |& if x < 0\\e^{x} &if  x \geq 0\end{cases}$

        $f_{2}(x)=x^{2},$

$f_{3}(x)=\begin{cases}sin x &if  x < 0\\x &if  x \geq 0\end{cases}$

$f_{4}(x)=\begin{cases}f_{2}(f_{1}(x)) &if  x < 0\\f_{2}(f_{1}(x)) -1 &if  x \geq 0\end{cases}$

Answer:

Explanation:

(P) Plan

 (i)    For such  questions , we need to properly define the functions and then we draw their graphs.

  (ii)  From the graphs,we can examine the function for continuity differentiability , one-one and onto 

   $f_{1}(x)=\begin{cases}-x & x < 0\\e^{x} & x \geq 0\end{cases}$

        $f_{2}(x)=x^{2},x\geq0$

$f_{3}(x)=\begin{cases}sin x & x < 0\\x & x \geq 0\end{cases}$

$f_{4}(x)=\begin{cases}f_{2}(f_{1}(x)) & x < 0\\f_{2}(f_{1}(x)) -1 & x \geq 0\end{cases}$

 Now,   $f_{2}(f_{1}(x)=\begin{cases} x^{2},& x < 0\\e^{2x}, & x \geq 0\end{cases}$

$f_{4}=\begin{cases} x^{2},& x < 0\\e^{2x}-1, & x \geq 0\end{cases}$

 As f₄(x) is contiinuous

                $f'_{4}=\begin{cases} 2x,& x < 0\\2e^{2x}, & x > 0\end{cases}$

 $f'_{4}(0)$  is not defined

 Its range is [0, $\infty$]

 Thus, range= codomain =[0,$\infty$]  thus f₄  is onto.

 Also, horizontal line (drawn parallel to x-axis) meets  the curve more than once function is not one-one 

  (Q)  Plan  $f_{3}(x)$

   differentiable at x=0  and not one-one

  As evident,  from the graph it is  continuous and no sharp turn at X=0 , thus f(x)  is  differentiable  at x=0

 Also, a horizontal line intersects the graph more than once.

 $\therefore$    It is not one-one

 (R)   Plan $f_{2}(f_{1}(x))$

 It is neither continuous nor one-one.

 From the graph , it can be observed that the function is not continuous at x=0

  Also , the horizontal line intersect,the curve at more than one point So,  $f_{2}(f_{1}(x))$ , is not one-one

(S) f₂(x)

 It is continuous  and one-one

 As evident from graphs , the function is continuous 

 also, the function is one-one , as any horizontal line  will meet the graph  only one 

$P\rightarrow(i), Q\rightarrow(iii),R\rightarrow(ii),S\rightarrow(iv)$ 

Match the list I with List II  and selected the correct answer using the codes given below the lists.

Answer:

Explanation:

(P)   $y=\cos (3\cos^{-1}x)$

     $y'=\frac{3 \sin(3\cos^{-1}x)}{\sqrt{1-x^{2}}}$

$\sqrt{1-x^{2}}y'=3\sin (3\cos ^{-1}x)$

  $\Rightarrow$    $ \frac{-x}{\sqrt{1-x^{2}}}y'+\sqrt{1-x^{2}} $  y''

  = $3\cos (3\cos^{-1}x).\frac{-3}{\sqrt{1-x^{2}}}  $

 $\Rightarrow $    $-xy'+(1-x^{2})y''=-9y $

$\Rightarrow   $  $\frac{1}{y}[(x^{2}-1)y'+xy']=9$

(Q)  Plan

  (i) Angle subtended by a side of n sided regular polygon at the centre =  $\frac{2\pi}{n}$

  (ii)  |a xb|=|a||b| $\sin\theta$

(iii) |a.b|=|a||b| $\cos\theta$

  (iv)  $\tan\theta=\tan\alpha\Rightarrow\theta=n\pi+\alpha,n\epsilon Z$

 consider a polygon of (S) n sides with centre at origin

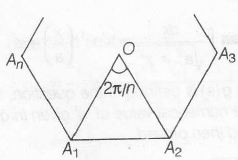
 Let |OA₁|=|OA₂|=......|OA_n|

 =r(say)

 |a_k  x a_k+1|=  $r^{2}\sin\frac{2\pi}{n}$

 |a_k  .a_k+1|=  $r^{2}\cos\frac{2\pi}{n}$

$\Rightarrow |\sum_{k=1}^{n-1}a_{k}\times a_{k+1}|=|\sum_{k=1}^{n-1} a_{k}.a_{k+1}|$

$\Rightarrow$  $ r^{2}(n-1)\sin\frac{2\pi}{n}=r^{2}(n-1)\cos \frac{2\pi}{n}$

$\tan \frac{2\pi}{n}=1$

$\Rightarrow$    $\tan \frac{2\pi}{n}=\tan\frac{\pi}{4}$

$\Rightarrow$    $\frac{2\pi}{n}=t\pi+\frac{\pi}{4},t\epsilon Z$

$\Rightarrow$     $\frac{2}{n}=\frac{4t+1}{4}$

  $\Rightarrow$     $ n=\frac{8}{4t+1},t\epsilon Z$

$\Rightarrow$    the minimum  value of n=8

 (R)   Plan Equation of  normal at the point 

   $(a \cos\theta,b\sin\theta)$   of ellipse   $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ is 

given by

$ax \sec\theta-bycosec\theta=a^{2}-b^{2}$

Equation of normal is

 $\sqrt{6}x\sec\theta-\sqrt{3}y cosec \theta=3$

 Its slope is

  $\frac{\sqrt{6}sec\theta}{\sqrt{3}cosec \theta}=1$

 ( $\therefore$   slope of normal = slope of line perpendicular to

  x+y=8

   $\tan\theta=\frac{1}{\sqrt{2}}$

 So, normal is

  $\sqrt{6}\times\frac{\sqrt{3}}{\sqrt{2}}-\sqrt{3}\times\sqrt{3}y=3$

 3x-3y=3

$\Rightarrow$    x-y=1

 As it passes through (h,l)

 So, h-1=1

    h=2

 (S) Plan

$\tan^{-1}x+\tan^{-1} y=\tan^{-1}\left(\frac{x+y}{1-xy}\right)$

 Given equation,

 $\tan^{-1} \left(\frac{1}{2x+1}\right)+\tan^{-1} \left(\frac{1}{4x+1}\right)=\tan^{-1} \left(\frac{2}{x^{2}}\right)$

= $\tan^{-1}  \left(\frac{\frac{1}{2x+1}+\frac{1}{4x+1}}{1-\frac{1}{(2x+1)(4x+1)}}\right)=\tan^{-1} \left(\frac{2}{x^{2}}\right)$

$\Rightarrow \tan^{-1}\left(\frac{6x+2}{(2x+1)(4x+1)-1}\right)= \tan^{-1}\left(\frac{2}{x^{2}}\right)$

$\Rightarrow$    $ \frac{3x+1}{4x^{3}+3x}=\frac{2}{x^{2}}$

$\Rightarrow $    $3x^{3}+x^{2}=8x^{2}+6x$

$\Rightarrow$    $ x(3x^{2}-7x-6)=0$

$\Rightarrow $     $x(x-3)(3x+2)=0$

$\Rightarrow $    $x=0,\frac{-2}{3},3$

 So, only positive solution is x=3

   P:(iv), Q:(iii), R:(ii), S(i)

Match the following

Answer:

Explanation:

(P) Plan

 (i)  A polymer satisfying  the given conditions is taken

  (ii)  The other  conditions are also applied and the number of polynomial  is taken out

 Let f(x)  =ax²+bx+c

   f(0)= 0 $\Rightarrow$ c=0

 Now, $\int_{0}^{1} f(x) dx=1$

    $\Rightarrow$     $ \left(\frac{ax^{3}}{3}+\frac{bx^{2}}{2}\right)_0^1=1$

$\Rightarrow$    $ \frac{a}{3}+\frac{b}{2}=1$

  $\Rightarrow$     $ 2a+3b=6$

 As a,b are non-negative integers

 So, a=0, b=2,  or a=3, b=0

 So, f(x)=2x  or f(x)=3x²

(Q)   Plan such type of questions are converted into only sine or cosine expression and then the number of points of maximum in given interval are obtained

     f(x)  = sin(x²)+ cos (x²)

       =  $\sqrt{2}\left[\frac{1}{\sqrt{2}}\cos (x^{2})+\frac{1}{\sqrt{2}}\sin(x^{2})\right]$

     =    $\sqrt{2}\left[\cos x^{2}\cos \frac{\pi}{4}+\sin\frac{\pi}{4}\sin(x^{2})\right]$

=$\sqrt{2}\cos (x^{2}-\frac{\pi}{4})$

 For maximum value

         $x^{2}-\frac{\pi}{4}=2n\pi$

  $\Rightarrow$     $ x^{2}=2n\pi+\frac{\pi}{4}$

$\Rightarrow$    $ x=\pm \sqrt{\frac{\pi}{4}},for n=0$

   $ x=\pm \sqrt{\frac{9\pi}{4}},$    for n=1

 So, f(x) attains  maximum at 4 points  in   $(-\sqrt{13},\sqrt{13})$

  (R)   Plan

  (i)    $\int_{-a}^{a} f(x) dx=\int_{-a}^{a} f(-x) dx$

  (ii)  $\int_{-a}^{a} f(x) dx=2\int_{0}^{a} f(x) dx$

    f(-x) =f(x)  , i.e, f is an even function

      $I= \int_{-2}^{2} \frac{3x^{2}}{1+e^{x}}dx$

  $I= \int_{-2}^{2} \frac{3x^{2}}{1+e^{-x}}dx$

$2I= \int_{-2}^{2} \left(\frac{3x^{2}}{1+e^{x}}+\frac{3x^{2}(e^{x})}{e^{x}+1}\right) dx$

    $2I= \int_{-2}^{2}3x^{2}dx$

  $\Rightarrow  $     $2I=2 \int_{0}^{2}3x^{2}dx$

      $I=[x^{3}]_0^2=8$

  (S)   Plan    $\int_{-a}^{a} f(x) dx=0$

  if f(-x)= -f(x)

 i.e, f(x) is an odd function

  Let f(x)= cos 2x  $\log\left(\frac{1+x}{1-x}\right)$

f(-x)= cos 2x  $\log\left(\frac{1-x}{1+x}\right)$

  =-f(x)

 Hence, f(x)  is an odd function.

 So,   $\int_{-1/2}^{1/2} f(x) dx=0$

 P:ii, Q:iii, R:i, S:iv

Given that for each   $a \epsilon (0,1), \lim_{h \rightarrow 0}$ $\int_{h}^{1-h}  t^{-a}(1-t)^{a-1}dt$  exists. Let this limit be g(a). In addition , it is given that the function g(a) differentiable (0,1)

The value of g'(1/2) is 

Answer:

Explanation:

 Plan    $\int_{0}^{a}f(x) dx=\int_{0}^{a} f(a-x) dx $

 As g(a) is given, use the numerical value of "a" given in the question and then proved .

 Given that ,

     $g(a)=\int_{0}^{1} \frac{dt}{t^{a}(1-t)^{1-a}}$

 Clearly  , g(a)=g(1-a)

  [Using   $\int_{0}^{a}f(x) dx=\int_{0}^{a}  f(a-x)dx]$

 Now, differentiate w.r.t 'a' , we get

   g'(a) =g'(1-a)(-1)

 Now, for    $a=-\frac{1}{2}$ , we have

   $-g'(\frac{1}{2})=g'(\frac{1}{2})$

  So,  $g'(\frac{1}{2})=0$

Given that for each   $a \epsilon (0,1), \lim_{h \rightarrow 0}$ $\int_{h}^{1-h} t^{-a}(1-t)^{a-1}dt$  exists. Let this limit be g(a)  . In addition , it is given that the function g(a) differentiable (0,1)

 The value  of   $g(\frac{1}{2})$   is 

Answer:

Explanation:

Plan   $\int_{}^{} \frac{dx}{\sqrt{a^{2}-x^{2}}}=\sin^{-1}\left(\frac{x}{a}\right)+c$

 As g(a)  is defined in the question, first use the numerical value of 'a' given in the question and then proved.

 Given, g(a) $=\lim_{h \rightarrow 0}\int_{h}^{1-h}t^{-a} (1-t)^{a-1}dt$

  $\therefore$   g(1/2)

     $=\lim_{h \rightarrow 0+}\int_{h}^{1-h} t^{-1/2}(1-t)^{-1/2}dt$

  $= \int_{0}^{1} \frac{dt}{\sqrt{t-t^{2}}}=\int_{0}^{1} \frac{dt}{\sqrt{\frac{1}{4}-\left(t-\frac{1}{2}\right)^{2}}}$

   = $\sin^{-1}\left[\left(\frac{t-1/2}{1/2}\right)\right]^{1}_{0}$

       = $\sin^{-1}1-\sin^{-1}(-1)=\pi$

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014