Discussion Forum

1)

Match the list I with List II  and selected the correct answer using the codes given below the lists.

Answer:

Option A

Explanation:

(P)   $y=\cos (3\cos^{-1}x)$

     $y'=\frac{3 \sin(3\cos^{-1}x)}{\sqrt{1-x^{2}}}$

$\sqrt{1-x^{2}}y'=3\sin (3\cos ^{-1}x)$

  $\Rightarrow$    $ \frac{-x}{\sqrt{1-x^{2}}}y'+\sqrt{1-x^{2}} $  y''

  = $3\cos (3\cos^{-1}x).\frac{-3}{\sqrt{1-x^{2}}}  $

 $\Rightarrow $    $-xy'+(1-x^{2})y''=-9y $

$\Rightarrow   $  $\frac{1}{y}[(x^{2}-1)y'+xy']=9$

(Q)  Plan

  (i) Angle subtended by a side of n sided regular polygon at the centre =  $\frac{2\pi}{n}$

  (ii)  |a xb|=|a||b| $\sin\theta$

(iii) |a.b|=|a||b| $\cos\theta$

  (iv)  $\tan\theta=\tan\alpha\Rightarrow\theta=n\pi+\alpha,n\epsilon Z$

 consider a polygon of (S) n sides with centre at origin

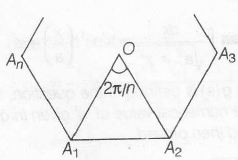
 Let |OA₁|=|OA₂|=......|OA_n|

 =r(say)

 |a_k  x a_k+1|=  $r^{2}\sin\frac{2\pi}{n}$

 |a_k  .a_k+1|=  $r^{2}\cos\frac{2\pi}{n}$

$\Rightarrow |\sum_{k=1}^{n-1}a_{k}\times a_{k+1}|=|\sum_{k=1}^{n-1} a_{k}.a_{k+1}|$

$\Rightarrow$  $ r^{2}(n-1)\sin\frac{2\pi}{n}=r^{2}(n-1)\cos \frac{2\pi}{n}$

$\tan \frac{2\pi}{n}=1$

$\Rightarrow$    $\tan \frac{2\pi}{n}=\tan\frac{\pi}{4}$

$\Rightarrow$    $\frac{2\pi}{n}=t\pi+\frac{\pi}{4},t\epsilon Z$

$\Rightarrow$     $\frac{2}{n}=\frac{4t+1}{4}$

  $\Rightarrow$     $ n=\frac{8}{4t+1},t\epsilon Z$

$\Rightarrow$    the minimum  value of n=8

 (R)   Plan Equation of  normal at the point 

   $(a \cos\theta,b\sin\theta)$   of ellipse   $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ is 

given by

$ax \sec\theta-bycosec\theta=a^{2}-b^{2}$

Equation of normal is

 $\sqrt{6}x\sec\theta-\sqrt{3}y cosec \theta=3$

 Its slope is

  $\frac{\sqrt{6}sec\theta}{\sqrt{3}cosec \theta}=1$

 ( $\therefore$   slope of normal = slope of line perpendicular to

  x+y=8

   $\tan\theta=\frac{1}{\sqrt{2}}$

 So, normal is

  $\sqrt{6}\times\frac{\sqrt{3}}{\sqrt{2}}-\sqrt{3}\times\sqrt{3}y=3$

 3x-3y=3

$\Rightarrow$    x-y=1

 As it passes through (h,l)

 So, h-1=1

    h=2

 (S) Plan

$\tan^{-1}x+\tan^{-1} y=\tan^{-1}\left(\frac{x+y}{1-xy}\right)$

 Given equation,

 $\tan^{-1} \left(\frac{1}{2x+1}\right)+\tan^{-1} \left(\frac{1}{4x+1}\right)=\tan^{-1} \left(\frac{2}{x^{2}}\right)$

= $\tan^{-1}  \left(\frac{\frac{1}{2x+1}+\frac{1}{4x+1}}{1-\frac{1}{(2x+1)(4x+1)}}\right)=\tan^{-1} \left(\frac{2}{x^{2}}\right)$

$\Rightarrow \tan^{-1}\left(\frac{6x+2}{(2x+1)(4x+1)-1}\right)= \tan^{-1}\left(\frac{2}{x^{2}}\right)$

$\Rightarrow$    $ \frac{3x+1}{4x^{3}+3x}=\frac{2}{x^{2}}$

$\Rightarrow $    $3x^{3}+x^{2}=8x^{2}+6x$

$\Rightarrow$    $ x(3x^{2}-7x-6)=0$

$\Rightarrow $     $x(x-3)(3x+2)=0$

$\Rightarrow $    $x=0,\frac{-2}{3},3$

 So, only positive solution is x=3

   P:(iv), Q:(iii), R:(ii), S(i)