JEE 2014 :: Advanced 2014 :: Mathematics 2014

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014

Let  $f:R\rightarrow R $   and     $g:R\rightarrow R $ be respectively given by f(x)=|x|+1 and g(x)=x²+1

 Define  h:R→ R by   $\begin{cases}max(f(x),g(x)) &if x \leq 0\\min(f(x),g(x)) &if x > 0\end{cases}$

The number  of points at which h(x) is not differentiable is 

Answer:

Explanation:

 Plan 

 (i)  In these type of questions, we  draw the graph of the function

 (ii)  The points at which the curve has taken a sharp turn, are the points of non-differentiability

 Curve of f(x) and g(x)  are 

 h (x)  is not  differentiable at  $x\pm1$    and 0

 As h(x) take sharp  turns  at $x\pm1 $   and 0 

 Hence, the number of points of non- differentiability of h(x) is 3.

The largest value of the non-negative integer a for which $\lim_{x \rightarrow 1}\left\{\frac{-ax+\sin(x-1)+a}{x+\sin(x-1)-1}\right\}^{\frac{1-x}{1-\sqrt{x}}}=\frac{1}{4} is 

Answer:

Explanation:

Plan $\lim_{x \rightarrow 0}\frac{\sin x}{x}=1$

 Given,  $\lim_{x \rightarrow 1}\left\{\frac{\sin (x-1)+a(1-x)}{(x-1)+\sin (x-1)}\right\}^{\frac{(1+\sqrt{x})(1-\sqrt{x})}{(1-\sqrt{x})}}=\frac{1}{4}$

 $\lim_{x \rightarrow 1}\left\{\frac{\frac{\sin(x-1)}{(x-1)}-a}{1+\frac{\sin(x-1)}{(x-1)}}\right\}^{1+\sqrt{x}}=\frac{1}{4}$

$\Rightarrow$       $\left(\frac{1-a}{2}\right)^{2}=\frac{1}{4}$

$\Rightarrow$    (a-1)²=1

$\Rightarrow$      a=2 or 0

 But for a=2 base of above limit approaches -1/2 and exponent approaches to 2 and since base cannot be negative. Hence limit does not exist

Let   $f:[0,4\pi]\rightarrow [0,\pi]$     be defined by $ f(x)=\cos^{-1}(\cos x)$  . The number of points  $x \in [0,4\pi]$  satisfying the equation   $f(x)=\frac{10-x}{10}$   is 

Answer:

Explanation:

Plan

   (i)    Using definition of f(x)= $\cos^{-1}(x)$  . we trace  the curve  $f(x)= \cos^{-1}(\cos x)$ 

  (ii)   The number of solutions of an equation involving trigonometric functions and algebraic function. algebraic  and algebraic functions are found using graphs of the curves

   We know , $\cos^{-1}(\cos x)$   = $\begin{cases}x & if x\in[0,\pi]\\2\pi-x & if x\in[\pi,2\pi] \\-2\pi+x&if x\in[2\pi,3\pi]  \\ 4\pi-x &if x \in[3\pi,4\pi]\end{cases}$

 From above figure. it is clear that   $y=\frac{10-x}{10}$    and   $y=\cos^{-1}(\cos x)$  intersect  at three distinct points, so number of solution is 3.

The  slope of the tangent to the curve   $(y-x^{5})^{2}=x(1+x^{2})^{2}$ at the point (1,3) is 

Answer:

Explanation:

 Plan

 Slope  of tangent  at the point   $(x_{1},y_{1})$  is     $ \left(\frac{dy}{dx}\right)_{(x_{1},y_{1})}$

 Given curve                    $(y-x^{5})^{2}=x(1+x^{2})^{2}$

 $\Rightarrow   2(y-x^{5})\left(\frac{\text{d}y}{\text{d}x}-5x^{4}\right)=(1+x^{2})^{2}+2x(1+x^{2}).2x$

  Put x=1, y=3   

$\therefore$           $\frac{dy}{dx}=8$

Let   $a \in R $    and   $f:R\rightarrow R$   be given by f(x)= x⁵ -5x+a,Then,

Answer:

Explanation:

Plan

     (i) Concepts of curve tracing are used in this question

   (ii) Number of roots are taken out from the curve traced

 Let     $y=x^{5}-5x$

    (i)    As   $x\rightarrow \infty$ ,$y\rightarrow \infty$   and as $x\rightarrow -\infty $, $y\rightarrow -\infty$.

    (ii)  Also,  at x=0 , y=0 , thus the curve passes through the origin.

 (iii)          $\frac{dy}{dx}=5x^{4}-5=5(x^{4}-1)$

                         $= 5(x^{2}-1)(x^{2}+1)$

       $= 5(x-1)(x+1)(x^{2}+1)$

 Now,   $\frac{dy}{dx}>0$    in     $(-\infty,-1) \cup (1,\infty)$

 thus  f(x) is increasing in these interval

 Also,   $\frac{dy}{dx}<0$     in (-1,1)  thus decreasing in (-1,1)

 (iv) Also, at x=-1,   $\frac{dy}{dx}$   change s its sign from +ve to -ve

 $\therefore$  x=-1 is point of local maxima .

 Similarly, x=1 is point  of local minima

 Local  maximum  value,

   $y=(-1)^{5}-5(-1)=4$

 Local minimum value

  $y=(-1)^{5}-5(1)=-4$

  Now, let y= -a

 As , evident from the graph, if   $-a\in (-4,4)i.e, a \in(-4,+4)$

 Then, f(x)  has three real roots and if -a >4  or -a <-4.

   then  f(x) has one real root.

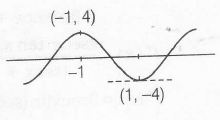
i.e, for a <-4  or a >4 , f(x) has one real root.

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014