Discussion Forum

1)

Let  $f:R\rightarrow R$   and     $g:R\rightarrow R$ be respectively given by f(x)=|x|+1 and g(x)=x²+1

 Define  h:R→ R by   $\begin{cases}max(f(x),g(x)) &if x \leq 0\\min(f(x),g(x)) &if x > 0\end{cases}$

The number  of points at which h(x) is not differentiable is 

Answer:

Option B

Explanation:

 Plan 

 (i)  In these type of questions, we  draw the graph of the function

 (ii)  The points at which the curve has taken a sharp turn, are the points of non-differentiability

 Curve of f(x) and g(x)  are 

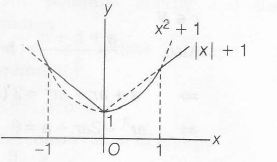
 h (x)  is not  differentiable at  $x\pm1$    and 0

 As h(x) take sharp  turns  at $x\pm1$   and 0 

 Hence, the number of points of non- differentiability of h(x) is 3.