Discussion Forum



1)

Let   $f:[0,4\pi]\rightarrow [0,\pi]$     be defined by $ f(x)=\cos^{-1}(\cos x)$  . The number of points  $x \in [0,4\pi]$  satisfying the equation   $f(x)=\frac{10-x}{10}$   is 


A) 4

B) 2

C) 3

D) 1

Answer:

Option C

Explanation:

Plan

   (i)    Using definition of f(x)= $\cos^{-1}(x)$  . we trace  the curve  $f(x)= \cos^{-1}(\cos x)$ 

  (ii)   The number of solutions of an equation involving trigonometric functions and algebraic function. algebraic  and algebraic functions are found using graphs of the curves

   We know , $\cos^{-1}(\cos x)$   = $\begin{cases}x & if x\in[0,\pi]\\2\pi-x & if x\in[\pi,2\pi] \\-2\pi+x&if x\in[2\pi,3\pi]  \\ 4\pi-x &if x \in[3\pi,4\pi]\end{cases}$

2432021373_cos.JPG

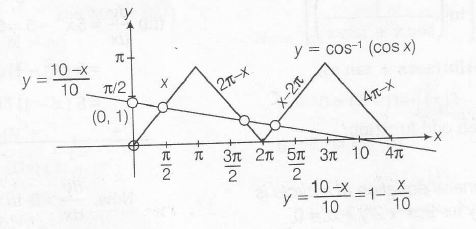
 From above figure. it is clear that   $y=\frac{10-x}{10}$    and   $y=\cos^{-1}(\cos x)$  intersect  at three distinct points, so number of solution is 3.