Discussion Forum

Let   $a \in R $    and   $f:R\rightarrow R$   be given by f(x)= x⁵ -5x+a,Then,

Answer:

Explanation:

Plan

     (i) Concepts of curve tracing are used in this question

   (ii) Number of roots are taken out from the curve traced

 Let     $y=x^{5}-5x$

    (i)    As   $x\rightarrow \infty$ ,$y\rightarrow \infty$   and as $x\rightarrow -\infty $, $y\rightarrow -\infty$.

    (ii)  Also,  at x=0 , y=0 , thus the curve passes through the origin.

 (iii)          $\frac{dy}{dx}=5x^{4}-5=5(x^{4}-1)$

                         $= 5(x^{2}-1)(x^{2}+1)$

       $= 5(x-1)(x+1)(x^{2}+1)$

 Now,   $\frac{dy}{dx}>0$    in     $(-\infty,-1) \cup (1,\infty)$

 thus  f(x) is increasing in these interval

 Also,   $\frac{dy}{dx}<0$     in (-1,1)  thus decreasing in (-1,1)

 (iv) Also, at x=-1,   $\frac{dy}{dx}$   change s its sign from +ve to -ve

 $\therefore$  x=-1 is point of local maxima .

 Similarly, x=1 is point  of local minima

 Local  maximum  value,

   $y=(-1)^{5}-5(-1)=4$

 Local minimum value

  $y=(-1)^{5}-5(1)=-4$

  Now, let y= -a

 As , evident from the graph, if   $-a\in (-4,4)i.e, a \in(-4,+4)$

 Then, f(x)  has three real roots and if -a >4  or -a <-4.

   then  f(x) has one real root.

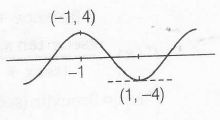
i.e, for a <-4  or a >4 , f(x) has one real root.