MHT CET 2017 :: Mathematics :: General questions

• Mathematics - General questions

The equation of liner equality inclined to coordinate axes and passing through (-3,2,-5) is 

Answer:

Explanation:

Let (x₁,y₁,z₁) =(-3,2,-5)

It is also given that, the line is equally inclined to coordinate axes,

 $\therefore$    l=-1,m=1 and n=-1

 We know that , the equation of line passing through (x₁,y₁,z₁) and having cosines l,m, n is 

$\frac{x-x_{1}}{l}=\frac{y-y_{1}}{m}=\frac{z-z_{1}}{n}$

$\therefore$      $\frac{x+3}{-1},\frac{y-2}{1},\frac{z+5}{-1}$

If f(x) =f(t)  and  y= g(t) are differentiable functions of t, then $\frac{d^{2}y}{dx^{2}}$  is 

Answer:

Explanation:

 Given , x=f(t) and y=g(t)

 On digfferentiating  both sides w.r.t 't' , we get

$\frac{dx}{dt}=f'(t) $and  $ \frac{dy}{dt}=g'(t)$

 We know that,  $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$

 $\Rightarrow$    $\frac{dy}{dx}=\frac{g'(t)}{f'(t)}$

 Again, differentiating both sides w.r.t 'x' , we get

 $\frac{d^{2}y}{dx^{2}}=\frac{f'(t).g''(t)-g'(t).f''(t)}{(f'(t))^{2}}.\frac{dt}{dx}$

    =$\frac{f'(t).g''(t)-g'(t).f''(t)}{(f'(t))^{2}}.\frac{1}{f'(t)}$

                               $  =\frac{f'(t).g''(t)-g'(t).f''(t)}{(f'(t))^{3}}$

The solution of the differential equation $\frac{dy}{dx}=\tan\left(\frac{y}{x}\right)+\frac{y}{x}$  is 

Answer:

Explanation:

 Given, 

 $\frac{dy}{dx}=\tan\left(\frac{y}{x}\right)+\frac{y}{x}$ ..........................(i)

 Clearly , the given different equation is homogeneous

 On putting y=Vx

$\frac{dy}{dx}=V+x\frac{dV}{dx}$     in Eq.(i) we get

 $V+x\frac{dV}{dx}=\tan V+V$

 $\Rightarrow$    $x\frac{dV}{dx}=\tan V$

 $\Rightarrow$      $\frac{1}{\tan V}dV=\frac{1}{x}dx$

On integrating both sides, we get

$\int \frac{1}{\tan V}dV=\int\frac{1}{x}dx$

$\Rightarrow$   $\int \cot VdV=\log x+\log c$

$\Rightarrow$     log sin x = log x+ log c

$\Rightarrow$   log sin V= log(xc)

$\Rightarrow$   sin v=xc

$\therefore$     $\sin (\frac{y}{x})=xc$

If the function  $f(x) =\left[ \tan \left(\frac{\pi}{4}+x\right)\right]^{1/x}$    for x≠0 is K for x=0 continuous at x =0, then K = ?

Answer:

Explanation:

We have , $f(x) =\left[ \tan \left(\frac{\pi}{4}+x\right)\right]^{1/x}$ =K

 Since , f(x)  is continuous at x=0, then

 $f(o)=\lim_{x \rightarrow 0}f(x)$

  $=\lim_{x \rightarrow 0}\left[ \tan \left(\frac{\pi}{4}+x\right)\right]^{1/x}$

$\Rightarrow K=\lim_{x \rightarrow 0}\left[\frac{1+\tan x}{1-\tan x}\right]^{1/x}$    [$1^{\infty}$ form]

$=e^{\lim_{x \rightarrow 0}\left[\frac{1+\tan x}{1-\tan x}-1\right].\frac{1}{x}}$

   $=e^{\lim_{x \rightarrow 0}\left[\frac{2\tan x}{1-\tan x}\right].\frac{1}{x}}$

 $=e^{2\lim_{x \rightarrow 0}\frac{\tan x}{x}.\lim_{x \rightarrow 0}\frac{1}{1-\tan x}}$

                                     $\left[\because \lim_{x\rightarrow 0}\frac{\tan x}{x}=1\right]$

 $\therefore$      $K=e^{2.1(\frac{1}{1-0})}=e^{2}$

O(0,0) , A(1,2) , B(3,4)  are the vertices of $\triangle OAB$. The joint equation of the altitude and median drawn from O is 

Answer:

Explanation:

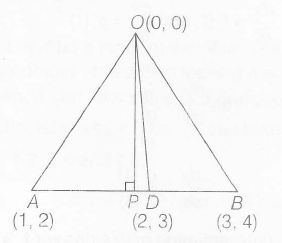
 Given , O(0,0) , A(1,2) and  B(3,4) be the vertices of $\triangle $ OAB

Let OP and OD be the altitude and median of $\triangle$ OAB, respectively

 $\therefore$   Coordinates of D= Mid of AB.=  $\left(\frac{1+3}{2},\frac{2+4}{2}\right)=\left(\frac{4}{2},\frac{6}{2}\right)=(2,3)$

 Now, ewquation of OD is (y-0)=  $\left(\frac{3-0}{2-0}\right)(x-0)$

                        $\left[\because y-y_{1}=\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1}\right)\right]$

$\Rightarrow$      $y=\frac{3}{2}x\Rightarrow2y=3x\Rightarrow3x-2y=0$

Slope of Op = -1/ Slope of AB                 $[\because  OP\bot AB]$

                           =$\frac{-1}{\left(\frac{3-1}{4-2}\right)}=\frac{-1}{\frac{2}{2}}=-1$

 $\therefore$ Equation of Op is (y-0) =-1(x-0)

                                             $[\because   y-y_{1}=slope (x-x_{1})]$

$\Rightarrow$     $y=-x\Rightarrow x+y=0$

 Now, joint equation of OP and OD

  (x+y)(3x-2y)=0

 $\Rightarrow$     3x²-2xy+3xy-2y²=0

$\Rightarrow$   $3x^{2}+xy-2y^{2}=0$

• Mathematics - General questions