TS EAMCET 2019 :: Mathematics :: General questions

• Mathematics - General questions

If the function f:R→ r  defined by

$f(x)=\begin{cases}a\left(\frac{1-\cos 2x}{x^{2}}\right), & for x < 0\\b ,& x = 0\\\frac{\sqrt{x}}{\sqrt{4+\sqrt{x}}-2}&for x>0\end{cases}$

 is continuous  at x=0 , then  a+b=

Answer:

Explanation:

We have, 

  $f(x)=\begin{cases}a\left(\frac{1-\cos 2x}{x^{2}}\right), & for x < 0\\b ,& x = 0\\\frac{\sqrt{x}}{\sqrt{4+\sqrt{x}}-2}&for x>0\end{cases}$

f(x) is continuous at x=0

 $\therefore$   $\lim_{x \rightarrow{0^{-}}}f(x)= f(0)$

$\lim_{x \rightarrow{0^{-}}}\frac{a(1- \cos 2x)}{x^{2}}=b$

$\lim_{x \rightarrow{0^{}}}\frac{a(2 \sin^{2} x)}{x^{2}}=b$

 $\Rightarrow$   2a=b

 Also,    $\lim_{x \rightarrow{0^{+}}}f(x)=b$

 $\therefore$     $\lim_{x \rightarrow{0^{}}}\frac{\sqrt{x}}{\sqrt{4+\sqrt{x-2}}}=b$

 $\Rightarrow\lim_{x \rightarrow{0^{}}}\frac{\sqrt{x}(\sqrt{4+\sqrt{x}}+2)}{\sqrt{x}}=b$

$\Rightarrow$   4=b , a=2

 $\therefore$ a+b=2+4=6

If  a triangle ABC with two vertices A(5,4,6) and B(1,-1,3) has its centroid  at ($\frac{10}{3},2,\frac{11}{3})$ then the third vertex C is 

Answer:

Explanation:

 We have $\triangle$ ABC

 A=(5,4,6). B=(1,-1,3), C=(x,y,z)

 Centroid of $\triangle$ ABC is    $\left(\frac{10}{3},2, \frac{11}{3}\right)$

$\therefore$      $\frac{10}{3} = \frac{5+1+x}{3} \Rightarrow   x=4$

                   $2= \frac{4-1+y}{3} \Rightarrow   y=3$

                 $\frac{11}{3}=  \frac{6+3+z}{3} \Rightarrow  z=2$

 $\therefore$   Vertices  C= (4,3,2)

If the locus of a point which divides a chord with slope 2 of the parabola $y^{2}=4x$ , internally in the ratio 1:3 is a parabola , then its vertes is 

Answer:

Explanation:

 Let   $P( t_{1}^{2},2t_{1})$    and    $Q( t_{2}^{2},2t_{2})$  are extremetre of chord

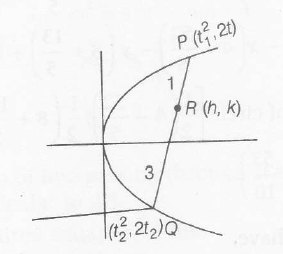
$\therefore$        $h=\frac{3 t_{1}^{2}+t_{2}^{2}}{4},k=\frac{6t_{1}+2t_{2}}{4}$

.Slope of PQ=2

 $\therefore$    $2=\frac{2t_{1}-2t_{2}}{t_{1}^{2}-t_{2}^{2}}$

 $t_{1}+t_{2}=1 $  $\Rightarrow  t_{2}=1-t_{1}$

 Put the value of $t_{2}$ in h and k , we get

 $4h=3 t_{1}^{2}+(1-t_{1})^{2}, 4k=6t_{1}+2-2t_{1}$

 $4h=4t_{1}^{2}-2t_{1}+1, 4k=4t_{1}+2$

 Eliminating $t_{1}$ , we get

$4h=4\left(\frac{2k-1}{2}\right)^{2}-2\left(\frac{2k-1}{2}\right)+1$

 $4h=4k^{2}-6k+3$

 $\Rightarrow$     $\left(k-\frac{3}{4}\right)^{2}=4\left(h-\frac{3}{16}\right)$

 $\therefore$    Vertex  ($\frac{3}{16},\frac{3}{4})$

The equation of a circle  concentric with the circle $x^{2}+y^{2}-6x+12y+15=0$ and having area that is twice the area of the given circle is 

Answer:

Explanation:

Given, 

$x^{2}+y^{2}-6x+12y+15=0$

 centre (3,-6)

    $r= \sqrt{9+36-15}= \sqrt{30}$

Area = $\pi (\sqrt{30})^{2}=30 \pi$

 Required equation of circle has twice the area of circle

$\therefore$     $A'= 60 \pi$

 $\pi R^{2}=60 \pi , R^{2}=60$

$\therefore$  Equation of circle concentric with given circle is 

 $(x-3)^{2}+(y+6)^{2}=60$

$x^{2}+y^{2}-6x+12y-15=0$

Let   $\lim_{t \rightarrow 0}(1+5t)^{1/t}=K$ and X be the random variable representing number of successes in 100 independent trails .If the probability  of success in each trial is 0.05  ,then the probability of getting  at least  one success is 

Answer:

Explanation:

We have

  $\lim_{t \rightarrow 0}(1+5t)^{1/t}=K$

 $\Rightarrow$     $K= e^{\lim_{t \rightarrow 0}\frac{5t}{t}}=e^{5}$

 Here, n=100 , p=0.05

 $\lambda$=np=5

$P(X\geq1)=1-P(X=0)=1-e^{-5}$

$P(X\geq1)=\frac{e^{5}-1}{e^{5}}=\frac{K-1}{K}$

• Mathematics - General questions