Answer:
Option D
Explanation:
Let P(t21,2t1) and Q(t22,2t2) are extremetre of chord
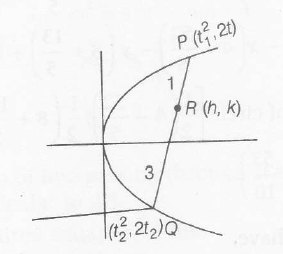
∴ h=3t21+t224,k=6t1+2t24
.Slope of PQ=2
∴ 2=2t1−2t2t21−t22
t1+t2=1 ⇒t2=1−t1
Put the value of t2 in h and k , we get
4h=3t21+(1−t1)2,4k=6t1+2−2t1
4h=4t21−2t1+1,4k=4t1+2
Eliminating t1 , we get
4h=4(2k−12)2−2(2k−12)+1
4h=4k2−6k+3
⇒ (k−34)2=4(h−316)
∴ Vertex (316,34)