JEE 2015 :: Advanced 2015 :: Mathematics 2015

• Advanced 2015 - Physics 2015
• Advanced 2015 - Chemistry 2015
• Advanced 2015 - Mathematics 2015

Consider the hyperbola H: x²-y²=1 and a circle S with centre N(x₂,0). Suppose that H and S touch each other at a point P(x₁,y₁) with x₁>1 and y₁>0. The common tangent to H and  S at P intersects the X-axis  at point M.  If  (l,m) is the centroid of $\triangle PMN$, then the correct expression(s) is/are

Answer:

Explanation:

Equation of family of circles touching hyperbola at (x₁,y₁) is

 (x-x₁)²+(y-y₁)²+λ(x x₁-y y₁-1)=0

 Now, its centre is (x₂,0).

$\therefore$  $\left[\frac{-(\lambda x_{1}-2x_{1)}}{2},-\frac{(-2y_{1}-\lambda y_{1})}{2}\right]=(x_{2},0)$

   $\Rightarrow $     $2y_{1}+\lambda y_{1}=0\Rightarrow\lambda=-2$

 and $2x_{1}-\lambda x_{1}=2x_{2}\Rightarrow x_{2}=2x_{1}$

  $\therefore $      $P(x_{1},\sqrt{x_1^2-1)}$

 And    $   N(x_{2},0)=(2x_{1},0)$

  As tangent intersect X-axis at  $M(\frac{1}{x},0)$

  Centroid of   $\triangle PMN=(l,m)$

 $\Rightarrow$      $\left(\frac{3x_{1}-\frac{1}{x_{1}}}{3},\frac{y_{1}+0+0}{3}\right)=(l,m)$

  $\Rightarrow l= \frac{3x_{1}+\frac{1}{x_{1}}}{3} $

 On differentiating w.r.t x₁, we get

     $\frac{dl}{dx_{1}}=\frac{3-\frac{1}{x_1^2}}{3}$

    $\Rightarrow$     $\frac{dl}{dx_{1}}=1-\frac{1}{3x_1^2},$ for   $x_{1}>1$

 and             $m=\frac{\sqrt{x_1^2-1}}{3}$

    On differentiating w.r.t x₁  , we get

$\frac{dm}{dx_{1}}=\frac{2x_{1}}{2\times 3\sqrt{x_1^2-1}}=\frac{x_{1}}{ 3\sqrt{x_1^2-1}}$,        for $x_{1}>1 $   

also    $m=\frac{y_{1}}{3}$

  On differentiating  w.r.t y₁, we get

      $\frac{dm}{dy_{1}}=\frac{1}{3},$    for   $y_{1}>0  $

 Let E₁  and E₂  be two ellipse whose centres are at the origin. The major axes of E₁ and E₂ lie along the lie X-axis and Y-axis, respectively. Let S be the circle   $x^{2}+(y-1)^{2}=2$ . The straight-line x+y=3 touches the curve S. E₁ and E₂ at P,Q and R, respectively. Suppose that  PQ=PR= $\frac{2\sqrt{2}}{3}$. If e₁ and e₂ are eccentricities  of E₁ and E₂ respectively, then the correct expression(s) is/are

Answer:

Explanation:

Here,    $E_{1}:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1,(a>b)$

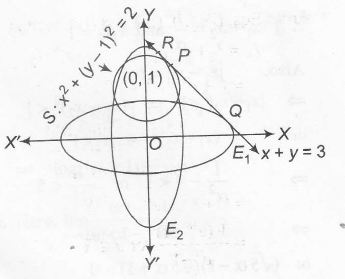
$E_{2}:\frac{x^{2}}{c^{2}}+\frac{y^{2}}{d^{2}}=1,(c<d)$

 and    $S:x^{2}+(y-1)^{2}=2$

 as tangent   to E₁ ,E₂ and S  is x+y=3.

 Let the point of contact of tangent be (x1,y1) to S.

$\therefore$  x.x₁+y.y₁-(y+y₁)+1=2

or   $xx_{1}+yy_{1}-y=(1+y_{1})$   , same as x+y=3.

 $\Rightarrow$         $\frac{x_{1}}{1}=\frac{y_{1}-1}{1}=\frac{1+y_{1}}{3}$

i.e,       x₁=1   and y₁=2

  $\therefore$  P= (1,2)

Since, PR= PQ=  $\frac{2\sqrt{2}}{3}$. thus   by parametric form.

   $\frac{x-1}{-1/\sqrt{2}}=\frac{y-2}{1/\sqrt{2}}=\pm\frac{2\sqrt{2}}{3}$

  $\Rightarrow $         $\left(x=\frac{5}{3},y=\frac{4}{3}\right)$

                                            and                  $ \left(x=\frac{1}{3},y=\frac{8}{3}\right)$

  $\therefore$       $ Q=\left(\frac{5}{3},\frac{4}{3}\right)$ and     $R= \left(\frac{1}{3},\frac{8}{3}\right)$

  Now, equation of tangent at Q on ellipse E₁  is

  $\frac{x.5}{a^{2}.3}+\frac{y.4}{b^{2}.3}=1$

   On comparing with x+y=3, we get

  a² =5  and b²=4

$\therefore$        $e_1^2=1-\frac{b^{2}}{a^{2}}=1-\frac{4}{5}=\frac{1}{5}$  ......(i)

 Also equation of tangent at R on ellipse E₂  is

   $\frac{x.1}{a^{3}.3}+\frac{y.8}{b^{2}.3}=1$

 On comparing with x+y=3, we get

    a²=1, b²=8

       $\therefore$        $e_2^2=1-\frac{a^{2}}{b^{2}}=1-\frac{1}{8}=\frac{7}{8}$  ......(ii)

 Now,   $e_1^2 .e_2^2=\frac{7}{40}\Rightarrow e_{1}e_{2}=\frac{\sqrt{7}}{2\sqrt{10}}$

and        $e_1^2+e_2^2=\frac{1}{5}+\frac{7}{8}=\frac{43}{40}$

          $|e_1^2+e_2^2|=|\frac{1}{5}-\frac{7}{8}|=\frac{27}{40}$

 If   $\alpha=3$   $\sin^{-1}\left(\frac{6}{11}\right)$   and    $\beta=3\cos^{-1}\left(\frac{4}{9}\right)$  , where the inverse trigonometric  functions take only the principal values, then the correct option (s) is /are

Answer:

Explanation:

 Here,  $\alpha=3\sin^{-}\left(\frac{6}{11}\right)$

    and    $\beta=3\cos^{-1}\left(\frac{4}{9}\right)4$   as   $\frac{6}{11}>\frac{1}{2}$

   $\Rightarrow $     $ \sin^{-1} \left(\frac{6}{11}\right)>\sin^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{6}$

$\therefore$       $\alpha=3 \sin^{-1} \left(\frac{6}{11}\right)>\frac{\pi}{2}\Rightarrow\cos\alpha<0$

Now,    $\beta=3\cos^{-1}\left(\frac{4}{9}\right)$

As  $\frac{4}{9}<\frac{1}{2}\Rightarrow\cos^{-1}\left(\frac{4}{9}\right)>\cos^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{3}$

$\therefore$        $\beta=3\cos^{-1}\left(\frac{4}{9}\right)>\pi$

$\therefore$                        $\cos\beta<0$    and    $\sin\beta<0$

Now, $\alpha+\beta$  is slightly greater than  $\frac{3\pi}{2}$

     $\therefore$          $\cos(\alpha+\beta)>0$

Let S be the set if all non-zero real numbers  $\alpha$ such that the quadratic equation $ \alpha x^{2}-x+\alpha=0$ has two distinct real roots  x₁  and x₂ satisfying the inequality |x₁-x₂|<1. Which of the following interval(s) is /are a subset of S?

Answer:

Explanation:

 Given , x₁  and x₂ are roots of   $\alpha x^{2}-x+\alpha=0$

$\therefore$     $x_{1}+x_{2}=\frac{1}{\alpha}$   and    $x_{1}x_{2}=1$

 Also,  $|x_{1}-x_{2}|<1$

 $\Rightarrow$    $|x_{1}-x_{2}|^{2}<1\Rightarrow(x_{1}-x_{2})^{2}<1$

 or         $(x_{1}-x_{2})^{2}-4x_{1}x_{2}<1$

 $\Rightarrow$    $\frac{1}{\alpha^{2}}-4<1$    or     $\frac{1}{\alpha^{2}}<5$

 $\Rightarrow$     $5\alpha^{2}-1>0$

or         $(\sqrt{5}\alpha-1)(\sqrt{5}\alpha+1)>0$

$\therefore$     $\alpha \epsilon \left(-\infty, -\frac{1}{\sqrt{5}}\right)\cup\left(\frac{1}{\sqrt{5}},\infty\right)$            ......(i)

 Also,            D>0

           $\Rightarrow$      $1-4\alpha^{2}>0$    or    $\alpha \epsilon \left(-\frac{1}{2},\frac{1}{2}\right)$ .....(ii)

 From Eqs. (i) and (ii) , we get

  $\alpha \epsilon \left(-\frac{1}{2}, -\frac{1}{\sqrt{5}}\right)\cup\left(\frac{1}{\sqrt{5}},\frac{1}{2}\right)$

Let  $f'(x)=\frac{192x^{3}}{2+\sin^{4}\pi x}$ for all x ε R with  $f(\frac{1}{2})=0$   If   $m\leq\int_{1/2}^{1} f(x) dx\leq M,$ , then the possible values of m and M are

Answer:

Explanation:

(b)

             Here,   $f'(x)=\frac{192x^{3}}{2+\sin^{4}\pi x}$

$\therefore$             $\frac{192x^{3}}{3}\leq f'(x)\leq \frac{192x^{3}}{2}$

 On integrating between the limits   $\frac{1}{2}$   to x, we get

  $\int_{1/2}^{x} \frac{192x^{3}}{3}dx\leq\int_{1/2}^{x} f'(x) dx\leq\int_{1/2}^{x}\frac{192x^{3}}{2} dx$

              $\Rightarrow \frac{192}{12}\left(x^{4}-\frac{1}{16}\right)\leq f(x)-f(0)$ $\leq24x^{4}-\frac{3}{2}$

               $\Rightarrow 16x^{4}-1\leq f(x) \leq24x^{4}-\frac{3}{2}$

 Again integrating  between the limits   $\frac{1}{2}$   to 1, we get

      $\int_{1/2}^{1} (16x^{4}-1)dx\leq\int_{1/2}^{1} f(x) dx\leq\int_{1/2}^{1} \left(24x^{4}-\frac{3}{2}\right)dx$

   $\Rightarrow$            $\left[\frac{16x^{5}}{5}-x\right]_{1/2}^1\leq \int_{1/2}^{1} f(x) dx$

                                                                                        $\leq\left[\frac{24x^{5}}{5}-\frac{3}{2}x\right]_{1/2}^1$

     $\Rightarrow$    $\left(\frac{11}{2}+\frac{2}{5}\right)\leq\int_{1/2}^{1}f(x) dx\leq\left(\frac{33}{10}+\frac{6}{10}\right) $

     $\Rightarrow$    $2.6\leq  \int_{1/2}^{1}  f(x) dx\leq3.9$

• Advanced 2015 - Physics 2015
• Advanced 2015 - Chemistry 2015
• Advanced 2015 - Mathematics 2015