Discussion Forum

Consider the hyperbola H: x²-y²=1 and a circle S with centre N(x₂,0). Suppose that H and S touch each other at a point P(x₁,y₁) with x₁>1 and y₁>0. The common tangent to H and  S at P intersects the X-axis  at point M.  If  (l,m) is the centroid of $\triangle PMN$, then the correct expression(s) is/are

Answer:

Explanation:

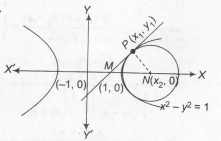
Equation of family of circles touching hyperbola at (x₁,y₁) is

 (x-x₁)²+(y-y₁)²+λ(x x₁-y y₁-1)=0

 Now, its centre is (x₂,0).

$\therefore$  $\left[\frac{-(\lambda x_{1}-2x_{1)}}{2},-\frac{(-2y_{1}-\lambda y_{1})}{2}\right]=(x_{2},0)$

   $\Rightarrow $     $2y_{1}+\lambda y_{1}=0\Rightarrow\lambda=-2$

 and $2x_{1}-\lambda x_{1}=2x_{2}\Rightarrow x_{2}=2x_{1}$

  $\therefore $      $P(x_{1},\sqrt{x_1^2-1)}$

 And    $   N(x_{2},0)=(2x_{1},0)$

  As tangent intersect X-axis at  $M(\frac{1}{x},0)$

  Centroid of   $\triangle PMN=(l,m)$

 $\Rightarrow$      $\left(\frac{3x_{1}-\frac{1}{x_{1}}}{3},\frac{y_{1}+0+0}{3}\right)=(l,m)$

  $\Rightarrow l= \frac{3x_{1}+\frac{1}{x_{1}}}{3} $

 On differentiating w.r.t x₁, we get

     $\frac{dl}{dx_{1}}=\frac{3-\frac{1}{x_1^2}}{3}$

    $\Rightarrow$     $\frac{dl}{dx_{1}}=1-\frac{1}{3x_1^2},$ for   $x_{1}>1$

 and             $m=\frac{\sqrt{x_1^2-1}}{3}$

    On differentiating w.r.t x₁  , we get

$\frac{dm}{dx_{1}}=\frac{2x_{1}}{2\times 3\sqrt{x_1^2-1}}=\frac{x_{1}}{ 3\sqrt{x_1^2-1}}$,        for $x_{1}>1 $   

also    $m=\frac{y_{1}}{3}$

  On differentiating  w.r.t y₁, we get

      $\frac{dm}{dy_{1}}=\frac{1}{3},$    for   $y_{1}>0  $