Discussion Forum

Let S be the set if all non-zero real numbers  $\alpha$ such that the quadratic equation $ \alpha x^{2}-x+\alpha=0$ has two distinct real roots  x₁  and x₂ satisfying the inequality |x₁-x₂|<1. Which of the following interval(s) is /are a subset of S?

Answer:

Explanation:

 Given , x₁  and x₂ are roots of   $\alpha x^{2}-x+\alpha=0$

$\therefore$     $x_{1}+x_{2}=\frac{1}{\alpha}$   and    $x_{1}x_{2}=1$

 Also,  $|x_{1}-x_{2}|<1$

 $\Rightarrow$    $|x_{1}-x_{2}|^{2}<1\Rightarrow(x_{1}-x_{2})^{2}<1$

 or         $(x_{1}-x_{2})^{2}-4x_{1}x_{2}<1$

 $\Rightarrow$    $\frac{1}{\alpha^{2}}-4<1$    or     $\frac{1}{\alpha^{2}}<5$

 $\Rightarrow$     $5\alpha^{2}-1>0$

or         $(\sqrt{5}\alpha-1)(\sqrt{5}\alpha+1)>0$

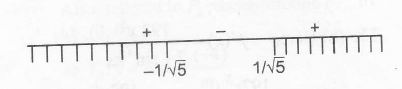
$\therefore$     $\alpha \epsilon \left(-\infty, -\frac{1}{\sqrt{5}}\right)\cup\left(\frac{1}{\sqrt{5}},\infty\right)$            ......(i)

 Also,            D>0

           $\Rightarrow$      $1-4\alpha^{2}>0$    or    $\alpha \epsilon \left(-\frac{1}{2},\frac{1}{2}\right)$ .....(ii)

 From Eqs. (i) and (ii) , we get

  $\alpha \epsilon \left(-\frac{1}{2}, -\frac{1}{\sqrt{5}}\right)\cup\left(\frac{1}{\sqrt{5}},\frac{1}{2}\right)$