JEE 2013 :: Advanced 2013 :: Chemistry 2013

• Advanced 2013 - Physics 2013
• Advanced 2013 - Chemistry 2013
• Advanced 2013 - Mathematics 2013

The standard  reduction potential data at 25° C  is given below.

$E^{0}(Fe^{3+}/Fe^{2+})=-0.77V$ ;

$E^{0}(Fe^{2}/Fe^{})=-0.44V$;

$E^{0}(Cu^{2+}/Cu)=+0.34V$;

$E^{0}(Cu^{+}/Cu)=+0.52V$;

$E^{0}(O_{2}(g)+4H^{+}+4e^{-})\rightarrow 2H_{2}O)=+1.23 V$

$E^{0}(O_{2}(g)+2H_{2}O+4e^{-})\rightarrow 4OH)=+0.40 V$

$E^{0}(Cr^{3+}/Cr^{})=-0.74V$ ;

$E^{0}(Cr^{2+}/Cr^{})=+0.91V$ ;

Match E°   of the rebox pair in List I with values given in list II and select the correct answer using the code given below the lists

Answer:

Explanation:

 plan when different number of electrons are involved in a redox reaction

 $\triangle G^{0}_{net}=\triangle G^{0}_{1}+\triangle G^{0}_{2}$

$-n_{3}FE^{0}_{3}=-n_{1}FE^{0}_{1}-n_{2}FE^{0}_{2}$

$E^{0}_{3}=\frac{n_{1}E^{0}_{1}+n_{2}E^{0}_{2}}{n_{3}}$

(P)     $E^{0}_{3+}Fe^{3+}/Fe$

Net reaction

 Fe³⁺→ Fe

 is obtained from  $\underline{n        E^{0}}$

Fe³⁺+e^-→  Fe ²⁺   n₁= 1,  $ E^{0d}_{1}=0.77V$

$Fe^{2+}+2e^{-}\rightarrow Fe , n_{2}=2, E^{0}_{2}=-0.44V$

$\because$   $Fe^{3+}+3e^{-}\rightarrow Fe , n_{3}=3, E^{0}_{3}=?$

    $E^{0}_{3}= \frac{n_{1}E^{0}_{1}+n_{2}E^{0}_{2}}{n_{3}}$

 =  $E^{0}_{3}= \frac{0.77+2(0.44)}{3}=\frac{-0.11}{3}=-0.04 V$

  Thus , P- (3)

   Net reaction

 $4H_{2}O\rightleftharpoons 4H^{+}+4OH^{-}$

 is obtained from      $\underline{n        E^{0}}$

 $2H_{2}O\rightarrow O_{2}$     n₁=4     E^o= -1.23 V

+ 4H⁺+4e^-

 $2H_{2}O+O_{2}+4e^{-}\rightarrow 4OH^{-}$     n₂=4  E^o=+0.40V

  $4H_{2}O\rightarrow 4H^{+}+4e^{-}$        n₃= 4      Eo= ?

$E_3^0=\frac{n_{1}E_1^0+n_{2}E_2^0}{n_{3}}=E_1^0+E_2^0$

  =-1.23+0.40= -0.83 V

 thus Q-(4)

(R)

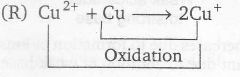
   Reduction

 for thus E° of Cu²⁺ →  Cu⁺

 is also required.      $\underline{n        E^{0}}$

 Cu²⁺+2e^-    →  Cu               n= 2         E^o=     0.34 V

 Cu →   Cu⁺ +e^-                      n=1         E^o= -0.52 V

  Cu²⁺  + e^-   →  Cu⁺            $E_3^0$        ?

 $E_3^0=\frac{n_{1}E_1^0+n_{2}E_2^0}{n_{3}}$

   $=\frac{2\times 0.34+1\times (0.52)}{1}=0.16 V$

 Thus                               $\underline{n        E^{0}}$

 Cu→  Cu⁺+e^-                   n1  =1    E^o=    -0.52 V

  Cu²⁺ + e^-→ Cu⁺            n₂ =1      E^o=  0.10 V

   Cu²⁺ +Cu→ 2Cu⁺           

 E⁰= -0.52 +0.16= -0.36 V

 thus (R)  - (1)

 (S)      Cr³⁺→ Cr²⁺ 

is obtained from          $\underline{n        E^{0}}$

Cr³⁺+3e^-→ Cr                n= 3                 E^o= -0.74 V

Cr→   Cr²⁺ +2e^-              n=2                  E^o=+0.91 V

 Cr³⁺+e^-→  Cr²⁺            n=1             E^o= ?

 $E_3^0=\frac{-0.74 \times3+2\times0.91}{1}=0.4 V$

  Thuus S= (2) 

P:3,Q:4,R:1,S:2

An aqueous solution of X is added slowly to an aqueous solution of Y as shown List I,  The variation in conductivity of these reactions is given in List II . Match List I   with List II  and selected the correct answer using  the code given below the lists 

Answer:

Explanation:

P:3, Q:4, R:2, S:1

Match the chemical conversion in list I  with the appropriate reagents in list II  and select the correct answer using the code given below the lists.

Answer:

Explanation:

P -(2) , Q- (3), R-(1), S-(4)

 The unbalanced chemical reactions give in list I show missing reagent or condition (?)  which are provided in list II. Match List I with List II  and select the correct answer using the code given below the lists 

Answer:

Explanation:

(P)   $2PbO_{2}+2H_{2}SO_{4}$    $\underrightarrow{warm(3)}$         $ 2PbSO_{4}+O_{2}+2H_{2}O$

(Q)    $Na_{2}S_{2}O_{3}+H_{2}O $     $\underrightarrow{Cl_{2}(4)}$ $NaHSO_{4}+HCl$

 (R)      $N_{2}H_{4} $   $\underrightarrow{I_{2}(2)}$  $ N_{2}+HI$

(S)     $XeF_{2}$        $\underrightarrow{NO(1)}$  Xe+NOF

 Thus , P - (3) , Q - (4), R- (2), S -(1)

The reactions of Cl₂  gas with cold-dilute and hot -concentrated NaOH in water give sodium salts of two (different)  oxoacids of chlorine, P and Q, respectively. The Cl₂ gas reacts with SO₂ gas , in the presence of charcoal, to give a product R. R reacts with  white phosphorous to give a  compound s, on hydrolysis, s gives an oxoacid of phosphorous T

 R, S and T respectively, are

Answer:

Explanation:

 Plan 2NaOH +Cl₂  $\underrightarrow {cold}$    $NaCl+NaOCl+H_{2}O$

                                                                          P

$6NaOH+3Cl_{2}$  $\underrightarrow {hot}$   $5NaCl+NaClO_{3}+3H_{2}O$

                                                                Q

$HOCl$    $\underrightarrow {NaOH}$     $NaOCl$

hypochlorous                             P

acid

 $Cl_{2}+SO_{2}\rightarrow SO_{2}Cl_{2}$

                                             R

 $10SO_{2}Cl_{2}+P_{4}\rightarrow 4PCl_{5}+ 10SO_{2}$

                                               S

$PCl_{5}+4H_{2}O\rightarrow H_{3}PO_{4}+ 5HCl$

                                            T

• Advanced 2013 - Physics 2013
• Advanced 2013 - Chemistry 2013
• Advanced 2013 - Mathematics 2013