Answer:
Option C
Explanation:
Due to current through side AB Magnetic field at the centre O
$B_{1}=\frac{\mu_{0}I}{4\pi a}[\sin \theta_{1}+\sin \theta_{2}]$
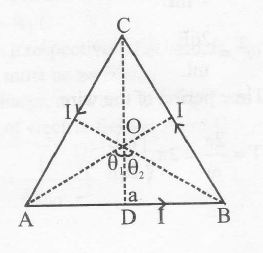
As the magnetic field due to each of the three sides is the same in magnitude and direction
$\therefore$ Total magnetic field at O is the sum of all the fields.
i.e, $B=3B_{1}=\frac{3\mu_{0}I}{4\pi a}[\sin \theta_{1}+\sin \theta_{2}]$
Here, $\tan\theta_{1}=\frac{AD}{OD}\Rightarrow\tan 60^{0}=\frac{\frac{l}{2}}{a}$
$a=\frac{l}{2\sqrt{3}}=\frac{9\times 10^{-2}}{2\sqrt{3}}$
Now B
$=3\times\frac{4\pi\times 10^{-7}\times2}{4\pi\times\frac{9\times 10^{-2}}{2\sqrt{3}}}[\sin 60^{0}+\sin 60^{0}]$
= $\frac{4\sqrt{3}}{9}\times 10^{-5}[\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}]$
=1.33 x 10-5 T