Discussion Forum

The earth is considered as a short magnet with its centre coinciding with the geometric centre of earth. The angle of dip $\phi$ related to the magnetic latitude  $\alpha\lambda$  as

Answer:

Explanation:

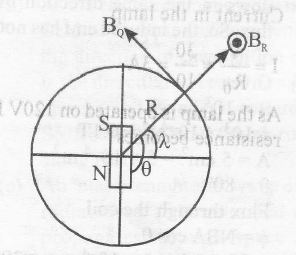
 For a dipole at position (R, Q)

 $B_{R}=\frac{\mu_{0}}{4\pi}.\frac{2M\cos\theta}{R^{3}}$   .....(i)

 and    $B_{Q}=\frac{\mu_{0}}{4\pi}.\frac{M\sin\theta}{R^{3}}$

 also   $\tan\phi=\frac{B_{V}}{B_{H}}=-\frac{B_{R}}{B_{Q}}$   ......(iii)

 Dividing eq.(i) by (ii)

 $\frac{B_{R}}{B_{Q}}=\frac{2\cos\theta}{\sin\theta}=2\cot\theta$    .....(iv)

 From eq.(iii) and (iv)

 $\tan\phi=-2\cot\theta$

From figure ,  $\theta=90^{0}+\lambda$

 $\because$     $\tan\phi=-2\cot(90+\lambda)$

$\tan\phi=2\tan\lambda$