Answer:
Option A
Explanation:
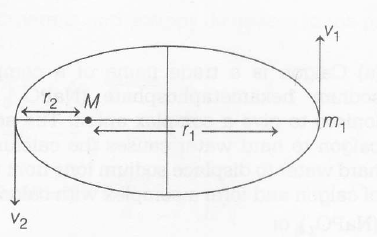
According to the law of conservation of angular momentum
$mv_{1}r_{1}=mv_{2}r_{2}$
$\Rightarrow$ $v_{2}=\frac{v_{1}r_{1}}{r_{2}}$ ...........(i)
From the law of conservation of total mechanical energy .
$\frac{-GMm}{r_{1}}+\frac{1}{2}mv_{1}^{2}=\frac{GMm}{r_{2}}+\frac{1}{2}mv_{2}^{2}$ .....(ii)
From Eqs.(i) and (ii) , we get
$v_{1}=\sqrt{\frac{2GMr_{2}}{(r_{1}+r_{2})r_{1}}}$
Angular momentum,
$L= mv_{1}r_{1}=m\left(\sqrt{\frac{2GMr_{2}}{(r_{1}+r_{2})r_{1}}}\right) \times r_{1}$
L= $m\sqrt{\frac{2GM_{}r_{1}r_{2}}{r_{1}+r_{2}}}$