Discussion Forum



1)

A planet of mass m moves in a elliptical orbit around an unknown star of mass M such that its maximum and minimum distances from the star are equal to $r_{1}$ and $r_{2}$ respectively. The angular momentum  of the planet relative to the centre of the star is 


A) $m\sqrt{\frac{2GM_{}r_{1}r_{2}}{r_{1}+r_{2}}}$

B) 0

C) $m\sqrt{\frac{2GM_{}(r_{1}+r_{2})}{r_{1}r_{2}}}$

D) $\sqrt{\frac{2GM_{}mr_{1}}{(r_{1}+r_{2})r_{2}}}$

Answer:

Option A

Explanation:

1182021775_m9.PNG

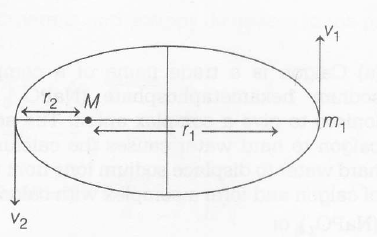
 According to the law of conservation  of angular momentum

   $mv_{1}r_{1}=mv_{2}r_{2}$

$\Rightarrow$       $v_{2}=\frac{v_{1}r_{1}}{r_{2}}$   ...........(i)

 From the law of conservation  of total mechanical energy .

 $\frac{-GMm}{r_{1}}+\frac{1}{2}mv_{1}^{2}=\frac{GMm}{r_{2}}+\frac{1}{2}mv_{2}^{2}$  .....(ii)

 From Eqs.(i) and (ii) , we get

$v_{1}=\sqrt{\frac{2GMr_{2}}{(r_{1}+r_{2})r_{1}}}$

Angular momentum,

    $L= mv_{1}r_{1}=m\left(\sqrt{\frac{2GMr_{2}}{(r_{1}+r_{2})r_{1}}}\right) \times r_{1}$

L= $m\sqrt{\frac{2GM_{}r_{1}r_{2}}{r_{1}+r_{2}}}$