JEE 2017 :: Advanced 2017 :: Physics 2017

• Advanced 2017 - Physics 2017
• Advanced 2017 - Chemistry 2017
• Advanced 2017 - Mathematics 2017

For an isosceles prism of angle A and refractive index μ, it is found that the angle of minimum deviation of $\delta_{m}=A$. Which of the following options is/are correct?

Answer:

Explanation:

The minimum deviation produced by a prism 

$\delta_{m}=2i-A=A$

$\therefore $   $i_{1}=i_{2}=A$  and  $r_{1}=r_{2}=\frac{A}{2}$

$\therefore $   $r_{1}=\frac{i_{1}}{2}$

  Now using Snell's law

 $\sin A= \mu \sin\frac{A}{2}$

  $\Rightarrow   \mu = 2\cos (A/2)$

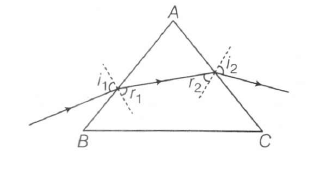
For this prism when the emergent ray at the second surface is tangential to the surface

$i_{2}=\frac{\pi}{2}$

$\therefore $  $r_{2}=\theta_{c}$

$\therefore $  $r_{1}=A-\theta_{c}$

so,  $\sin i_{1}=\mu \sin(A-\theta_{c})$

so,

  $i_{1}= \sin^{-1}[\sin A\sqrt{4\cos^{2}\frac{A}{2}-1}-cos A]$

 For minimum deviation through the isosceles prism, the ray inside the prism is parallel to the base of the prism  $\angle B=\angle C$

But it is not necessarily parallel to the base it.   $\angle A=\angle B$ or $\angle A=\angle C$

In the circuit shown L= 1μ H, C= 1μ F, and R= 1 kΩ. They are connected in series with an AC source V= V₀  sinωt as shown. Which of the following options is/are correct?

 ω

Answer:

Explanation:

At ω =0, $X_{c}=\frac{1}{\omega C}=\infty$  therefore  current  is  nearly zero.

   Further at the resonance frequency, current and voltage are in phase. This resonance frequency is given by

             $\omega_{r}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{10^{-6}\times10^{-6}}}=10^{6}rad/sec$

  We can see that this frequency is independent of R

 Further , X_L= ωL , X_C = $\frac{1}{\omega C}$

  At ω =ω_r   = 10⁶ rad/S, X_L=X_C . 

 For ω >ω_r , X_L > X_C.  So, the circuit is inductive.

• Advanced 2017 - Physics 2017
• Advanced 2017 - Chemistry 2017
• Advanced 2017 - Mathematics 2017