Discussion Forum



1)

For an isosceles prism of angle A and refractive index μ, it is found that the angle of minimum deviation of $\delta_{m}=A$. Which of the following options is/are correct?


A) For the angle of incidence $i_{1}=A$, the ray inside the prism is parallel to the base of the prism

B) At minimum deviation , the incident angle $i_{1}$ and refracting angle $r_{1}$ at the first refracting surface are realated by $r_{1}=(\frac{i_{1}}{2})$

C) For the prism, the emergent ray at the second surface will be tangent to the surface when the angle of incidence at the first surface is $i_{1}= \sin^{-1}[\sin A\sqrt{4\cos^{2}\frac{A}{2}-1}-cos A]$

D) For this prism, the refractive index $\mu$ and the angle prism A are related as $A=\frac{1}{2}\cos^{-1}(\frac{\mu}{2})$

Answer:

Option A,B,C

Explanation:

The minimum deviation produced by a prism 

$\delta_{m}=2i-A=A$

$\therefore $   $i_{1}=i_{2}=A$  and  $r_{1}=r_{2}=\frac{A}{2}$

$\therefore $   $r_{1}=\frac{i_{1}}{2}$

  Now using Snell's law

 $\sin A= \mu \sin\frac{A}{2}$

  $\Rightarrow   \mu = 2\cos (A/2)$

10122019995_CIRCL.PNG

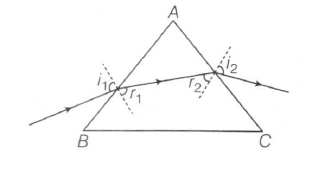
For this prism when the emergent ray at the second surface is tangential to the surface

$i_{2}=\frac{\pi}{2}$

$\therefore $  $r_{2}=\theta_{c}$

$\therefore $  $r_{1}=A-\theta_{c}$

so,  $\sin i_{1}=\mu \sin(A-\theta_{c})$

so,

  $i_{1}= \sin^{-1}[\sin A\sqrt{4\cos^{2}\frac{A}{2}-1}-cos A]$

 

 For minimum deviation through the isosceles prism, the ray inside the prism is parallel to the base of the prism  $\angle B=\angle C$

But it is not necessarily parallel to the base it.   $\angle A=\angle B$ or $\angle A=\angle C$