In a thin rectangular metallic strip, a constant current I flows along the positive x-direction, as shown in the figure. The length, width and thickness of the strip are l, w and d respectively. A uniform magnetic field B is applied on the strip along the positive y-direction. Due to this, the charge carriers experience a net deflection along the z-direction. This results in the accumulation of charge carries on the surface PQRS and the appearance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z-direction is thus developed. Charge accumulation continues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross-section of the strip and carried by electrons.
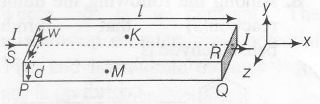
Consider two different metallic strips (1 and 2) of same dimensions (length l, width w and thickness d) with carrier densities n1 and n2, respectively. Strip 1 is placed in magnetic field B1 and strip 2 is placed in magnetic field B2, both along positive y- directions. Then V1 and V2 are the potential differences developed between K and M in strips 1 and 2, respectively. Assuming that the current I is the same for both the strips, the correct options is/are