Discussion Forum

A rectangular sheet of the fixed perimeter with sides having their lengths in the ratio 8:15 is converted into an open rectangular box by folding after removing squares of the equal area from all four corners.If the total area of removed squares is 100, the resulting box has maximum volume.The lengths of the sides of the rectangular sheet are 

Answer:

Explanation:

Concept involved

 The problem is based on the concept to maximize the volume of a cuboid

 i.e,  to form a function of volume , say f(x) find  f'(x)  and f"(x).

 Put f'(x) =0 and check f'(x)  to be +ve  or -ve for minimum and maximum, respectively

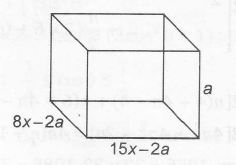
Here, l=15x-2a, b=8x-2a

 h=a

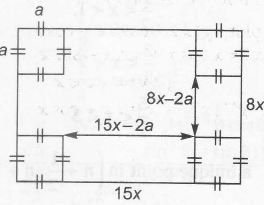
$\therefore$ Volume =(8x-2a)(15x-2a)a

 V=2a(4x-a)(15x-2a)....(i)

$\frac{dv}{da}=6a^{2}-46ax+60x^{2}$

$\frac{d^{2}v}{da^{2}}=12a-46x$

  Here,   $(\frac{dv}{da})=0$

$\Rightarrow $   $ 6x^{2}-23x+15=0$

 at   $a=5\Rightarrow x=3,\frac{5}{6}$

$\left(\frac{d^{2}v}{da^{2}}\right)=2(30-23x)$

at    x=3, $\left(\frac{d^{2}v}{da^{2}}\right)$ =2(30-69)<0

$\therefore$  Maximum when x=3,

 also at              $x=\frac{5}{6}\Rightarrow \left(\frac{d^{2}v}{da^{2}}\right)>0$

 $\therefore$  at   x=5/6 , volume is minimum

 Thus, sides are 8x=24  and 15 x=45