Discussion Forum

The position vector of A and B are $2\hat{i}+2\hat{j}+\hat{k}$ and $2\hat{i}+4\hat{j}+4\hat{k}$. The length of the internal bisector of <BOA triangle AOB is

Answer:

Explanation:

We have,

OA = |$2\hat{i}+2\hat{j}+\hat{k}$| = 3;

OB = |$2\hat{i}+4\hat{j}+4\hat{k}$| = 6

Since the internal bisector divides opposite side in the

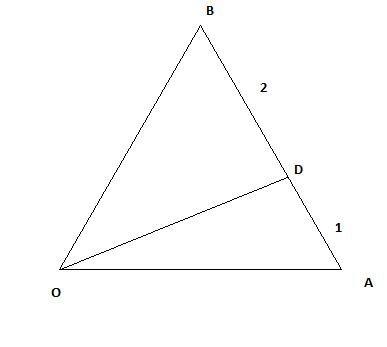
ratio of adjacent sides

$\frac{AC}{BC} = \frac{3}{6}=\frac{1}{2}$

where OD is the bisector of <BOA .

.'. The position vector of C is

$\frac{2(2\hat{i}+2\hat{j}+\hat{k})+(2\hat{i}+4\hat{j}+4\hat{k})}{2+1} $

=$2\hat{i}+\frac{8}{3}\hat{j}+2\hat{k}$

.'. OD = |$2\hat{i}+\frac{8}{3}\hat{j}+2\hat{k}$|

= $\sqrt{\frac{136}{9}}$