Discussion Forum

1)

A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60º and the refractive index of the material of prism is √3 then the angle of deviation of the ray is

 

 

Answer:

Option A

Explanation:

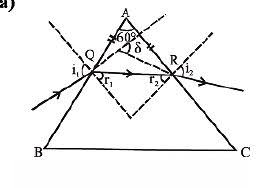
Given AQ = AR and $\angle A = 60^{0}$

$\therefore \angle AQR =\angle ARQ =  60^{0}$

$\therefore r_{1} = r_{2} = 30^{o}$

Applying Snell's law on face AB

$\sin i_{1} = \mu\sin r_{1}$

$\sin i_{1} = \sqrt{3}\sin 30^{o} = \sqrt{3}\times\frac{1}{2}$

= $\frac{\sqrt{3}}{2}$

$\therefore i_{1} = 60^{o} = i_{2}$

In a prism, deviation

$\delta =i_{1} + i_{2}-A$ = 60º + 60º - 60º = 60º