Mathematics | VITEEE 2018 | Discussion Page

The radius of the sphere $x^{2} +y^{2} +z^{2} =49,2x+3y-z-5\sqrt{14} =0$ is

$\sqrt{6}$

$2\sqrt{6}$

$4\sqrt{6}$

$6\sqrt{6}$

Option B

The sphere, $x^{2} +y^{2} +z^{2} =49$ has centre at the origin (0, 0, 0) and radius 7.

1052021955_VITEE M.JPG

DisTance of the plane $2x+3y-z-5\sqrt{14} =0$

from the origin

$\frac{|2(0)+3(0)-(0)-5\sqrt{14}|}{\sqrt{2^{2}+3^{2}+(-1)^{2}}}$

= $\frac{|-5\sqrt{14}|}{\sqrt{14}}$ = $\frac{5\sqrt{14}}{\sqrt{14}}$ = 5

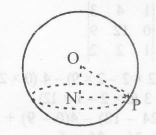
Thus in Figure ; OP = 7, ON = 5

NP²= OP² - ON² = 7² - 5² = 49 - 25 = 24

.'. NP = $2\sqrt{6}$ Hence the radius of the circle = NP = $2\sqrt{6}$

Discussion Forum