Discussion Forum



1)

Let A be the centre of the circle $x^{2}+y^{2}-2x-4y-20 =0$ and B( 1,7) and D(4,-2) are points on the circle then, if tangents be drawn on B and D which meet at C, then area of quadilateral ABCD is-


A) 150

B) 75

C) 75/2

D) None of these

Answer:

Option B

Explanation:

2562021152_cmglwllodryb-s.png

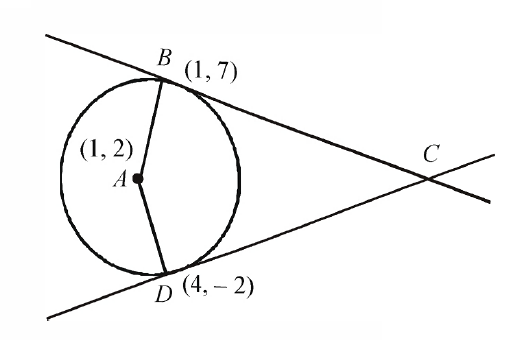
Here, Centre is A (1,2), and tangent B(1,7) is 

x.1 +y.7 - 1 (x+ 1)-2 (y+7)-20=0  or y = 7 ...(1)

Tangent at D (4,1) is 3x - 4y - 20 = 0 ...(2)

Solving ( 1 ) and (2),we get C is (16, 7)

Area ABCD = 2 (Area of Δ ABC) = 2 × 1/2 AB × BC = AB × BC = 5×15 =  75 UNITS