Answer:
Option C
Explanation:
The given lines are,
y - 1 = x, x ≥ 0;
y - 1 = -x, x<0
y = 0, x = -1/2, x < 0; x = 1/2, x ≥ 0
so that the area bounded is as shown in the figure.
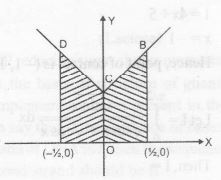
Required area = 2$\int_{0}^{1/2} (1+x).dx$ = 2$\left(x+\frac{x^{2}}{2}\right)_0^\frac{1}{2}$
= 2 (1/2 + 1/8) = 5/4