Answer:
Option B
Explanation:
The given point is on axis of $\frac{\overrightarrow{p}}{2}$ dipole and at equatorial line of $\overrightarrow{p}$ dipole so that field at given point is ($\overrightarrow{E_{1}}+\overrightarrow{E_{2}}$)
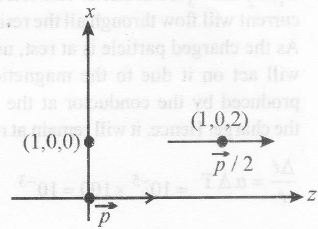
$\overrightarrow{E_{1}}=\frac{2K(p/2)}{2^{3}}=\frac{K_{p}}{8}(+\hat{k})$
$\overrightarrow{E_{2}}=\frac{K_{p}}{1}(-\hat{k})$
$\overrightarrow{E_{1}}+\overrightarrow{E_{2}}=-\frac{7}{8}K_{p}(-\hat{k})=\frac{-7 p}{32\pi\epsilon_{0}}\hat{k}$