Discussion Forum

1)

 In given circuit, C₁=C₂=C₃= C  initially Now a dielectric slab of dielectric constant   $K=\frac{3}{2}$  is inserted in C₂

 

The equivalent capacitance become

Answer:

Option A

Explanation:

 When dielectric slab of dielectric constant

 K= $\frac{3}{2} $ is  inserted between the plates of C₂,

 Its new capacitance (C₂') becomes

   C₂'= $\frac{3}{2}$ C

 Equivalent capacitance of C₂'  and C₃ is

 $C_{eq}=C_2'+C_{3}=\frac{3}{2}C+C=\frac{5C}{2}$

 

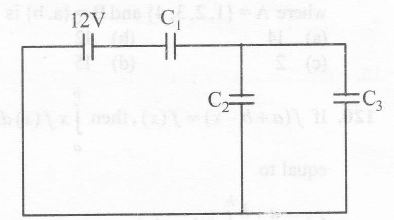
 Now , C_eq and C₁ are in series . Therefore , their equivalent capacitancce is 

$C_{eq}=\frac{C_{eq}\times C_{1}}{C_{eq}+ C_{1}}=\frac{\frac{5C}{2}\times C}{\frac{5C}{2}+C}$

  $=\frac{5C^{2}}{7C}=\frac{5C}{7}$