Discussion Forum

What is the area of loop of the curve r =a sin 3 $\theta$ ?

Answer:

Explanation:

If curve r = a sin3$\theta$

 To trace the curve , we consider the following table:

 Thus there is a loop between $\theta$ =0 &  $\theta=\frac{\pi}{3}$

 as r  varies from r=0 to r=0.

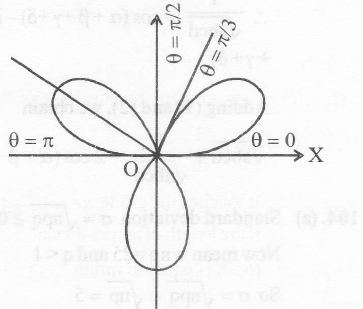
 Hence, the area of the loop lying in the

positive quadrant $=\frac{1}{2}\int_{0}^{\frac{\pi}{3}} r^{2}d\theta$

 $=\frac{1}{2}\int_{0}^{\frac{\pi}{3}}\sin^{2}\phi .\frac{1}{3}d\phi$

[on putting ,  $=3\theta=\phi\Rightarrow d\theta=\frac{1}{3}d\phi]$

$=\frac{a^{2}}{6}\int_{0}^{\frac{\pi}{2}} \sin^{2}\phi d\phi$

$=\frac{a^{2}}{6}\int_{0}^{\frac{\pi}{2}} \frac{1-\cos2\phi}{2}d\phi [\because \cos2\theta=1-2\sin^{2}\theta]$

$=\frac{a^{2}}{12}\left[\phi+\frac{\sin 2 \phi}{2}\right]^{\frac{\pi}{2}}_{0}$

$=\frac{a^{2}}{12}\left[\frac{\pi}{2}+\sin\pi\right]=\frac{a^{2}\pi}{24}$