Discussion Forum

Two points masses, m each carrying charges -q and +q are attached to the ends of a massless rigid non-conducting wire of length  'L'  . when this arrangement is placed in the uniform electric field, then it deflects through an angle i. The  minimum time  needed by rod to  align itself  along the field is 

Answer:

Explanation:

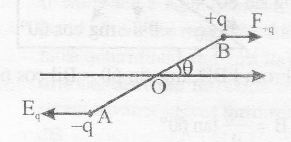
Torque  when the wire is brought in a uniform field E

$\tau= qEL\sin\theta$

= $ qEL\theta$       [ $\because$ $\theta$  is very small]

Moment of intertia  of rod AB about O

$I=m\left(\frac{L}{2}\right)^{2}+m\left(\frac{L}{2}\right)^{2}=\frac{mL^{2}}{2}$

$\tau= I\alpha$

$\therefore$     $\alpha=\frac{\tau}{I}=\frac{qEL\theta}{\frac{mL^{2}}{2}}$

$\Rightarrow $    $\omega^{2}\theta=\frac{2qEL\theta}{mL^{2}}[\because \theta=\omega^{2}\theta]$

$\Rightarrow \omega^{2}=\frac{2qE}{mL}$

 Time period of the wire

$T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{mL}{2qE}}$

The rod will become parallel to the field

in time T/4

$\therefore$     $t=\frac{T}{4}=\frac{\pi}{2}\sqrt{\frac{mL}{2qE}}$