Discussion Forum



1)

 A tetrahedron  has vertices at  O  (0,0,0) , A(1,-2,1) ,B(-2,1,1)  and C  (1,-1,2). Then the angle between the faces OAB and ABC will be


A) $\cos^{-1}\left(\frac{1}{2}\right)$

B) $\cos^{-1}\left(\frac{1}{6}\right)$

C) $\cos^{-1}\left(\frac{-1}{3}\right)$

D) $\cos^{-1}\left(\frac{1}{4}\right)$

Answer:

Option C

Explanation:

2852021205_v3.JPG

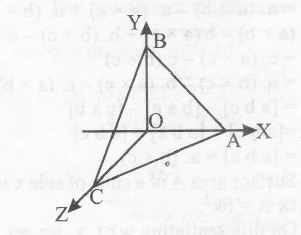
 Vector perpendicular  to face OAB=  $\overrightarrow{n_{1}}$

= $\overrightarrow{OA}\times\overrightarrow{OB}$

 =  $(\hat{i}-2\hat{j}+\hat{k})\times (-2\hat{i}+\hat{j}+\hat{k})$

=$(-2-1)\hat{i}-(-2-1)\hat{j}+(1-4)\hat{k})$

= $-3\hat{i}-3\hat{j}-3\hat{k}$

 Vector perpendicular to face ABC=  $\overrightarrow{n_{2}}$.

= $\overrightarrow{AB}\times\overrightarrow{AC}$

= $(-3\hat{i}+3\hat{j})\times  (\hat{j}+\hat{k})$

=   $-3\hat{i}+3\hat{j}-3\hat{k}$

 Since,  angle between faces is equal to angle between their normals.

$\therefore$  $\cos\theta=\frac{\overrightarrow{n_{1}}.\overrightarrow{n_{2}}}{|\overrightarrow{n_{1}}||\overrightarrow{n_{2}}|}$

 $= \frac{(-3)(3)+(-3)(3)+(-3)(-3)}{\sqrt{9+9+9}\sqrt{9+9+9}}$

$= \frac{-9-9+9}{\sqrt{27}\sqrt{27}}=-\frac{1}{3}$

$\Rightarrow\theta=\cos^{-1}(\frac{-1}{3})$