Answer:
Option B
Explanation:
Ley x denote the sum of the numbers obtained when two fair dice are rolled
So, X may have values 2,3,4,5,6,7,8,9,10,11 and 12
P(X=2)=P(1,1)=136
P(X=3)=P(1,2),(2,1)=236
P(X=4)=336, P(X=5)=436
P(X=6)=536, P(X=7)=636
P(X=8)=536,
P(X=9)=436,P(X=10)=336,P(X=11)=236,
P(X=12)=136,
∴ Probability distribution table is given below
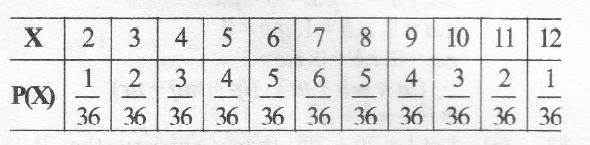
Mean¯X=∑XP(X)
=[2×1+3×2+4×3+5×4+6×5+7×6+8×5+9×4+10×3+11×2+12×1]36
=25236=7
Variance = ∑X2P(X)−¯X2
[22×1+32×2+42×3+52×4+62×5+72×6+82×5+92×4+102×3+112×2+122×1]36-72
=197436−49
=1974−176436
21036=356
∴ Variance =356
and SD=√356