Discussion Forum

 Consider a toroid with rectangular cross-section, of inner radius a,  outer radius b  and height h, carrying n number of turns. Then  the self-inductance of the toroidal  coil when  current I passing through the toroid is 

Answer:

Explanation:

 Given, a toroid with a rectangular cross-section of inner radius a  and outer radius b.

 Height of the solenoid=h

Magnetic field inside a rectangular toroid is given by

$B=\frac{\mu_{0}n^{}I}{2 \pi r}$   ................(i)

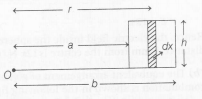
Using the infinitesimal cross-sectional area element,

  dx=h dr

 $\therefore$    Flux passing through  the cross-section of toroid 

$\phi=\int B.dx =\int_{a}^{b} \frac{\mu_{0}n^{}I}{2 \pi r}.(h dr)$

 $\phi= \frac{\mu_{0}n^{}Ih}{2 \pi }\int_{a}^{b} \frac{1}{r}. dr$

 $\Rightarrow$       $\phi= \frac{\mu_{0}n^{}Ih}{2 \pi }[\log r]_{a}^{b}$

 $\Rightarrow$       $\phi= \frac{\mu_{0}n^{}Ih}{2 \pi }  (\log b-\log a)$

                               $\phi= \frac{\mu_{0}n^{}Ih}{2 \pi }ln\left(\frac{b}{a}\right)$

 Now, self inductance  of rectangular toroid.

   $L= \frac{n \phi}{I}$

 Putting  the value  of $\phi_{}$ , we get

L=  $\frac{\mu_{0}n^{2}h}{2 \pi}ln\left(\frac{b}{a}\right)$