Discussion Forum

An iron rod of length 1.5 m lying on a horizontal table is pulled up from one end along a vertical line so as to move it with a constant velocity 3 m/s. while the other end of the rod slides along the floor. After how much time the speed of the end sliding  on the floor equals to the speed of the end being pulled up

Answer:

Explanation:

 According to question,

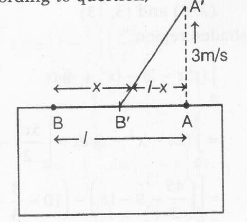
 Given,

AB is an iron rod whose length is given by

   l=1.5 m

 velocity of end A,

   v=3 m/s

Let t be the time when both the ends have same speed. since end A has always a constant velocity, therefore the velocity of end B at point B' is also become 3 m/s.

 In the position of B'A' of the rod, i.e, after time t,

 $(l-x)^{2}+(3t)^{2}=l^{2}$

 $(1.5-x)^{2}+9t^{2}=(1.5)^{2}$

 $2.25+x^{2}-3x+9t^{2}=2.25$

 $x^{2}-3x+9t^{2}=0$   ............(i)

 As rod is moving with a constant  velocity then from equation of the motion,

 $x=ut+\frac{1}{2}at^{2}$

 x=3t     .............(ii)

 [ $\because$  velocity ,u=3 m/s and accleration , a=0]

 From Eqs.(i) and (ii)

$(3t)^{2}-3(3t)+9t^{2}=0$

 $9t^{2}-9t+9t^{2}=0$

 $18t^{2}-9t=0 \Rightarrow t= \frac{1}{2}$