Discussion Forum

1)

A metal plate of thickness  2mm and area $36 \pi  cm^{2}$ is slide into a parallel plate capacitor of plate spacing 6 mm and are $36 \pi cm^{2}$ . The metal plate is at a distance 3 mm from one of the plates. What is the capacitance of this arrangement?  

$\left( Let\frac{1}{4 \pi \in_{0}}=9 \times 10^{9} Nm^{2}C^{-2}\right)$

Answer:

Option C

Explanation:

When metal plate of thickness 2mm is inserted into a parallel plate capacitor , then the arrangement is shown as,

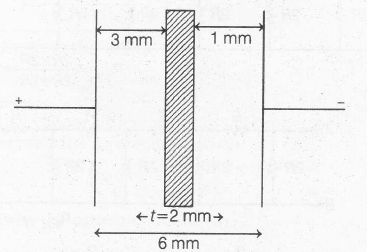
Given , thickness  of plate, t=2mm and area, A=$36 \pi cm^{2}$

The above circuit can be redrawn as,

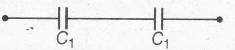
 where, $C_{1}=\frac{\epsilon_{0}A}{d_{1}}$  and $C_{2}=\frac{\epsilon_{0}A}{d_{2}}$

 Now, $ C_{eq}= \frac{C_{1}C_{2}}{C_{1}+C_{2}}$  (In the series combination)

$\Rightarrow C_{eq}=\epsilon_{0}A\left[\frac{\frac{1}{d_{1}}\times\frac{1}{d_{2}}}{\frac{1}{d_{1}}+\frac{1}{d_{2}}}\right]=\frac{\epsilon_{0}A}{d_{1}+d_{2}}$

$\Rightarrow C_{eq}=\frac{1}{4 \pi \times 9 \times 10^{9}}\times\frac{36 \pi \times 10^{-4}}{3\times 10^{-3}+1\times 10^{-3}}$

                               $\left( \because \frac{1}{4 \pi\epsilon_{0}}={ 9 \times 10^{9} Nm^{2}/C^{2}}\right)$

 =$\frac{1}{4} \times 10^{-10}$=$25 \times 10^{-12}$ F=25pF

so, the correct option is (c)