Discussion Forum

In Young's double-slit experiment , a thin sheet of refractive index  1.6 is used to cover one slit while a thin the sheet of refractive index  1.3 is used to cover the second slit. The thickness of both the sheets are same and the wavelength of light used in 600nm. If the central point on the screen is now occupied by what had been the 10th bright fringe (m=10)  , then the thickness of covering sheets is 

Answer:

Explanation:

Given, refractive index of first sheet $\mu_{1}$=1.6  refractive index of second sheet $\mu_{2}$=1.3 and  wavelength of light $\lambda$=600nm=$600 \times 10^{-9}$ m

 A young's double-slit experiment is shown below, in which two thin sheets have covered the slits . So, the path difference introduced in slit 1.

 $\triangle x_{1}=(\mu_{1}-1)t= (1.6-1)t=0.6t$

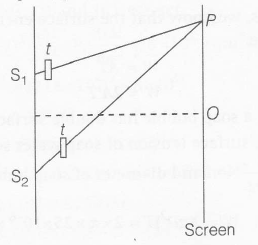
 Similarly , path difference introduced in slit 2,

 $\triangle x_{2}= (\mu _{2}-1)t=(1.3-1)t=0.3t$

 So, the net path difference introduced  in central maxima,

$\triangle x_{central maxima}=\triangle x_{1}-\triangle x_{2}$=0.6t-0.3t=0.3t

 For central maxima, which occupied the $10^{th}$ bright fringe,

$\triangle x_{cen}=10 \lambda$

$\Rightarrow$                 t= $\frac{10 \times 600 \times 10^{-9}}{0.3}-20\mu m$

Hence, the correct option is (c)